IB Questionbank

Updates to Questionbank

User interface language: English | Español

SL Paper 1

The volume of a hemisphere, V, is given by the formula

V = $\sqrt {\frac{{4\,{S^3}}}{{243\,\pi }}}$ ,

where S is the total surface area.

The total surface area of a given hemisphere is 350 cm².

Calculate the volume of this hemisphere in cm³.

Give your answer correct to one decimal place.

[3]

Write down your answer to part (a) correct to the nearest integer.

[1]

Write down your answer to part (b) in the form a × 10^k , where 1 ≤ a < 10 and k ∈ $\mathbb{Z}$ .

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\sqrt {\frac{{4\,{{\left( {350} \right)}^3}}}{{243\,\pi }}}$ OR $\sqrt {\frac{{171500\,000}}{{763.407\, \ldots }}}$ (M1)

Note: Award (M1) for substitution of 350 into volume formula.

= 473.973… (A1)

= 474 (cm³) (A1)(ft) (C3)

Note: The final (A1)(ft) is awarded for rounding their answer to 1 decimal place provided the unrounded answer is seen.

[3 marks]

474 (cm³) (A1)(ft) (C1)

Note: Follow through from part (a).

[1 mark]

4.74 × 10² (cm³) (A1)(ft)(A1)(ft) (C2)

Note: Follow through from part (b) only.

Award (A0)(A0) for answers of the type 0.474 × 10³.

[2 marks]

Examiners report

[N/A]

The following table shows the probability distribution of a discrete random variable $A$ , in terms of an angle $\theta$ .

M17/5/MATME/SP1/ENG/TZ1/10

Show that $\cos \theta = \frac{3}{4}$ .

[6]

Given that $\tan \theta > 0$ , find $\tan \theta$ .

[3]

Let $y = \frac{1}{{\cos x}}$ , for $0 < x < \frac{\pi }{2}$ . The graph of $y$ between $x = \theta$ and $x = \frac{\pi }{4}$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of summing to 1 (M1)

eg $\,\,\,\,\,$ $\sum {p = 1}$

correct equation A1

eg $\,\,\,\,\,$ $\cos \theta + 2\cos 2\theta = 1$

correct equation in $\cos \theta$ A1

eg $\,\,\,\,\,$ $\cos \theta + 2(2{\cos ^2}\theta - 1) = 1,{\text{ }}4{\cos ^2}\theta + \cos \theta - 3 = 0$

evidence of valid approach to solve quadratic (M1)

eg $\,\,\,\,\,$ factorizing equation set equal to $0,{\text{ }}\frac{{ - 1 \pm \sqrt {1 - 4 \times 4 \times ( - 3)} }}{8}$

correct working, clearly leading to required answer A1

eg $\,\,\,\,\,$ $(4\cos \theta - 3)(\cos \theta + 1),{\text{ }}\frac{{ - 1 \pm 7}}{8}$

correct reason for rejecting $\cos \theta \ne - 1$ R1

eg $\,\,\,\,\,$ $\cos \theta$ is a probability (value must lie between 0 and 1), $\cos \theta > 0$

Note: Award R0 for $\cos \theta \ne - 1$ without a reason.

$\cos \theta = \frac{3}{4}$ AG N0

valid approach (M1)

eg $\,\,\,\,\,$ sketch of right triangle with sides 3 and 4, ${\sin ^2}x + {\cos ^2}x = 1$

correct working

(A1)

eg $\,\,\,\,\,$ missing side $= \sqrt 7 ,{\text{ }}\frac{{\frac{{\sqrt 7 }}{4}}}{{\frac{3}{4}}}$

$\tan \theta = \frac{{\sqrt 7 }}{3}$ A1 N2

[3 marks]

attempt to substitute either limits or the function into formula involving ${f^2}$ (M1)

eg $\,\,\,\,\,$ $\pi \int_\theta ^{\frac{\pi }{4}} {{f^2},{\text{ }}\int {{{\left( {\frac{1}{{\cos x}}} \right)}^2}} }$

correct substitution of both limits and function (A1)

eg $\,\,\,\,\,$ $\pi \int_\theta ^{\frac{\pi }{4}} {{{\left( {\frac{1}{{\cos x}}} \right)}^2}{\text{d}}x}$

correct integration (A1)

eg $\,\,\,\,\,$ $\tan x$

substituting their limits into their integrated function and subtracting (M1)

eg $\,\,\,\,\,$ $\tan \frac{\pi }{4} - \tan \theta$

Note: Award M0 if they substitute into original or differentiated function.

$\tan \frac{\pi }{4} = 1$ (A1)

eg $\,\,\,\,\,$ $1 - \tan \theta$

$V = \pi - \frac{{\pi \sqrt 7 }}{3}$ A1 N3

[6 marks]

Examiners report

[N/A]

The diameter of a spherical planet is $6 \times 10^{4} km$ .

Write down the radius of the planet.

[1]

The volume of the planet can be expressed in the form $π (a \times 10^{k}) {km}^{3}$ where $1 \leq a < 10$ and $k \in ℤ$ .

Find the value of $a$ and the value of $k$ .

[3]

Markscheme

$3 \times 10^{4}$ OR $30000 (km)$ (accept $3 ∙ 10^{4}$ ) A1

[1 mark]

$\frac{4}{3} π {(3 \times 10^{4})}^{3}$ OR $\frac{4}{3} π {(30000)}^{3}$ (A1)

$= \frac{4}{3} π \times 27 \times 10^{12} (= π (36 \times 10^{12}))$ OR $= \frac{4}{3} π \times 27000000000000$ (A1)

$= π (36 \times 10^{13}) ({km}^{3})$ OR $a = 3.6, k = 13$ A1

[3 marks]

Examiners report

[N/A]

A line ${L_1}$ passes through the points ${\text{A}}(0,{\text{ }}1,{\text{ }}8)$ and ${\text{B}}(3,{\text{ }}5,{\text{ }}2)$ .

Given that ${L_1}$ and ${L_2}$ are perpendicular, show that $p = 2$ .

Find $\overrightarrow {AB}$ .

[2]

a.i.

Hence, write down a vector equation for ${L_1}$ .

[2]

a.ii.

A second line ${L_2}$ , has equation r = $\left( {\begin{array}{*{20}{c}} 1 \\ {13} \\ { - 14} \end{array}} \right) + s\left( {\begin{array}{*{20}{c}} p \\ 0 \\ 1 \end{array}} \right)$ .

Given that ${L_1}$ and ${L_2}$ are perpendicular, show that $p = 2$ .

[3]

The lines ${L_1}$ and ${L_1}$ intersect at $C(9,{\text{ }}13,{\text{ }}z)$ . Find $z$ .

[5]

Find a unit vector in the direction of ${L_2}$ .

[2]

d.i.

Hence or otherwise, find one point on ${L_2}$ which is $\sqrt 5$ units from C.

[3]

d.ii.

Markscheme

valid approach (M1)

eg $A - B,\,\, - \left( \begin{gathered} 0 \hfill \\ 1 \hfill \\ 8 \hfill \\ \end{gathered} \right) + \left( \begin{gathered} 3 \hfill \\ 5 \hfill \\ 2 \hfill \\ \end{gathered} \right)$

$\overrightarrow {AB} = \left( \begin{gathered} 3 \hfill \\ 4 \hfill \\ - 6 \hfill \\ \end{gathered} \right)$ A1 N2

[2 marks]

a.i.

any correct equation in the form r = a + tb (any parameter for $t$ ) A2 N2

where a is $\left( \begin{gathered} 0 \hfill \\ 1 \hfill \\ 8 \hfill \\ \end{gathered} \right)$ or $\left( \begin{gathered} 3 \hfill \\ 5 \hfill \\ 2 \hfill \\ \end{gathered} \right)$ , and b is a scalar multiple of $\left( \begin{gathered} 3 \hfill \\ 4 \hfill \\ - 6 \hfill \\ \end{gathered} \right)$

eg $\,\,\,\,\,$ r = $\left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 8 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 3 \\ 4 \\ { - 6} \end{array}} \right)$ , r = $\left( {\begin{array}{*{20}{c}} {3 + 3t} \\ {5 + 4t} \\ {2 - 6t} \end{array}} \right)$ , r = j + 8k + t(3i + 4j – 6k)

Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.

[2 marks]

a.ii.

valid approach (M1)

eg $\,\,\,\,\,$ $a \bullet b = 0$

choosing correct direction vectors (may be seen in scalar product) A1

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} 3 \\ 4 \\ { - 6} \end{array}} \right)$ and $\left( {\begin{array}{*{20}{c}} p \\ 0 \\ 1 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 3 \\ 4 \\ { - 6} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} p \\ 0 \\ 1 \end{array}} \right) = 0$

correct working/equation A1

eg $\,\,\,\,\,$ $3p - 6 = 0$

$p = 2$ AG N0

[3 marks]

valid approach (M1)

eg $\,\,\,\,\,$ ${L_1} = \left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ z \end{array}} \right),{\text{ }}{L_1} = {L_2}$

one correct equation (must be different parameters if both lines used) (A1)

eg $\,\,\,\,\,$ $3t = 9,{\text{ }}1 + 2s = 9,{\text{ }}5 + 4t = 13,{\text{ }}3t = 1 + 2s$

one correct value A1

eg $\,\,\,\,\,$ $t = 3,{\text{ }}s = 4,{\text{ }}t = 2$

valid approach to substitute their $t$ or $s$ value (M1)

eg $\,\,\,\,\,$ $8 + 3( - 6),{\text{ }} - 14 + 4(1)$

$z = - 10$ A1 N3

[5 marks]

$\left| {\vec d} \right| = \sqrt {{2^2} + 1} \,\,\left( { = \sqrt 5 } \right)$ (A1)

$\frac{1}{{\sqrt 5 }}\left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ 1 \end{array}} \right)\,\,\,\,\,\left( {{\text{accept}}\left( {\begin{array}{*{20}{c}} {\frac{2}{{\sqrt 5 }}} \\ {\frac{0}{{\sqrt 5 }}} \\ {\frac{1}{{\sqrt 5 }}} \end{array}} \right)} \right)$ A1 N2

[2 marks]

d.i.

METHOD 1 (using unit vector)

valid approach (M1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ { - 10} \end{array}} \right) \pm \sqrt 5 \hat d$

correct working (A1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ { - 10} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ 1 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 9 \\ {13} \\ { - 10} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ 1 \end{array}} \right)$

one correct point A1 N2

eg $\,\,\,\,\,$ $(11,{\text{ }}13,{\text{ }} - 9),{\text{ }}(7,{\text{ }}13,{\text{ }} - 11)$

METHOD 2 (distance between points)

attempt to use distance between $(1 + 2s,{\text{ }}13,{\text{ }} - 14 + s)$ and $(9,{\text{ }}13,{\text{ }} - 10)$ (M1)

eg $\,\,\,\,\,$ ${(2s - 8)^2} + {0^2} + {(s - 4)^2} = 5$

solving $5{s^2} - 40s + 75 = 0$ leading to $s = 5$ or $s = 3$ (A1)

one correct point A1 N2

eg $\,\,\,\,\,$ $(11,{\text{ }}13,{\text{ }} - 9),{\text{ }}(7,{\text{ }}13,{\text{ }} - 11)$

[3 marks]

d.ii.

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

d.i.

[N/A]

d.ii.

The points ${\text{A}}$ and ${\text{B}}$ have position vectors $\left( {\begin{array}{*{20}{c}} { - 2} \\ 4 \\ { - 4} \end{array}} \right)$ and $\left( {\begin{array}{*{20}{c}} 6 \\ 8 \\ 0 \end{array}} \right)$ respectively.

Point ${\text{C}}$ has position vector $\left( {\begin{array}{*{20}{c}} { - 1} \\ k \\ 0 \end{array}} \right)$ . Let ${\text{O}}$ be the origin.

Find, in terms of $k$ ,

$\overrightarrow {{\text{OA}}} \bullet \overrightarrow {{\text{OC}}}$ .

[2]

a.i.

$\overrightarrow {{\text{OB}}} \bullet \overrightarrow {{\text{OC}}}$ .

[1]

a.ii.

Given that ${\text{A}}\widehat {\text{O}}{\text{C}} = {\text{B}}\widehat {\text{O}}{\text{C}}$ , show that $k = 7$ .

[8]

Calculate the area of triangle ${\text{AOC}}$ .

[6]

Markscheme

correct substitution into either $\overrightarrow {{\text{OA}}} \bullet \overrightarrow {{\text{OC}}}$ or into $\overrightarrow {{\text{OB}}} \bullet \overrightarrow {{\text{OC}}}$ (in (ii)) (A1)

eg $- 2 \times \left( { - 1} \right) + 4 \times k$ , $6 \times \left( { - 1} \right) + 8 \times k$

correct expression A1 N1

eg $2 + 4k$ , $4k + 2$

[2 marks]

a.i.

correct expression A1 N1

eg $8k - 6$ , $- 6 + 8k$

[1 mark]

a.ii.

finding magnitudes (seen anywhere) A1A1

eg $\sqrt {{{\left( { - 2} \right)}^2} + {{\left( 4 \right)}^2} + {{\left( { - 4} \right)}^2}} \,\,\left( { = 6} \right)$ , $\sqrt {{{\left( 6 \right)}^2} + {{\left( 8 \right)}^2} + {0^2}} \,\,\left( { = 10} \right)$

correct substitution of their values into formula for angle ${\text{AOC}}$ (A1)

eg ${\text{cos}}\,\theta = \frac{{2 + 4k}}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( 4 \right)}^2} + {{\left( { - 4} \right)}^2}} \left| {\overrightarrow {{\text{OC}}} } \right|}}$

correct substitution of their values into formula for angle ${\text{BOC}}$ (A1)

eg ${\text{cos}}\,\theta = \frac{{8k - 6}}{{\sqrt {{{\left( 6 \right)}^2} + {{\left( 8 \right)}^2} + {0^2}} \left| {\overrightarrow {{\text{OC}}} } \right|}}$

recognizing that ${\text{cos}}\,{\text{A}}\widehat {\text{O}}{\text{C}} = {\text{cos}}\,{\text{B}}\widehat {\text{O}}{\text{C}}$ (seen anywhere) (M1)

eg $\frac{{2 + 4k}}{{\left| {\overrightarrow {{\text{OC}}} } \right|\sqrt {{{\left( { - 2} \right)}^2} + {{\left( 4 \right)}^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{8k - 6}}{{\left| {\overrightarrow {{\text{OC}}} } \right|\sqrt {{6^2} + {{\left( 8 \right)}^2} + {0^2}} }}$ , $\frac{{2 + 4k}}{{6\sqrt {1 + {k^2}} }} = \frac{{8k - 6}}{{10\sqrt {1 + {k^2}} }}$

correct working (without radicals) (A2)

eg $10\left( {2 + 4k} \right) = 6\left( {8k - 6} \right)$ , $11{k^2} - 79k + 14 = 0$

correct working clearly leading to the required answer A1

eg $20 + 36 = 48k$ , $56 = 8k$ , $k = 7$ and $k = \frac{2}{{11}}$ , $\left( {k - 7} \right)\left( {11k - 2} \right) = 0$

$k = 7$ AG N0

[8 marks]

finding magnitude of $\overrightarrow {{\text{OC}}}$ (seen anywhere) A1

eg $\sqrt {{{\left( { - 1} \right)}^2} + {7^2} + {0^2}}$ , $\sqrt {50}$

valid attempt to find ${\text{cos}}\,\theta$ (M1)

eg ${\text{cos}}\,\theta = \frac{{2 + 28}}{{6\sqrt {{{\left( { - 1} \right)}^2} + {7^2} + {0^2}} }}$ , ${\text{cos}}\,\theta = \frac{{56 - 6}}{{10\sqrt {{{\left( { - 1} \right)}^2} + {7^2} + {0^2}} }}$ , ${\left( {\sqrt {26} } \right)^2} = {6^2} + {\left( {\sqrt {50} } \right)^2} - 2\left( 6 \right)\sqrt {50} \,{\text{cos}}\,\theta$

finding ${\text{cos}}\,\theta$ A1

eg ${\text{cos}}\,\theta = \frac{5}{{\sqrt {50} }}\,\,\,\left( { = \frac{1}{{\sqrt 2 }}} \right)$

valid approach to find ${\text{sin}}\,\theta$ (seen anywhere) (M1)

eg $\theta = \frac{\pi }{4}$ , ${\text{sin}}\,\theta = {\text{cos}}\,\theta$ , ${\text{sin}}\,\theta = \sqrt {1 - \frac{{25}}{{50}}}$ , ${\text{sin}}\,\theta = \sqrt {1 - {\text{co}}{{\text{s}}^2}\,\theta }$ , ${\text{sin}}\,\theta = \frac{{\sqrt 2 }}{2}$

correct substitution of their values into $\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}$ (A1)

eg $\frac{1}{2} \times 6 \times \sqrt {50}$ , $\frac{1}{2} \times 6 \times \sqrt {50} \times \frac{5}{{\sqrt {50} }}$

area is $15$ A1 N3

[6 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

A balloon in the shape of a sphere is filled with helium until the radius is 6 cm.

The volume of the balloon is increased by 40%.

Calculate the volume of the balloon.

[2]

Calculate the radius of the balloon following this increase.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

Units are required in parts (a) and (b).

$\frac{4}{3}\pi \times {6^3}$ (M1)

Note: Award (M1) for correct substitution into volume of sphere formula.

$= 905{\text{ c}}{{\text{m}}^3}{\text{ }}(288\pi {\text{ c}}{{\text{m}}^3},{\text{ }}904.778 \ldots {\text{ c}}{{\text{m}}^3})$ (A1) (C2)

Note: Answers derived from the use of approximations of $\pi$ (3.14; 22/7) are awarded (A0).

[2 marks]

Units are required in parts (a) and (b).

$\frac{{140}}{{100}} \times 904.778 \ldots = \frac{4}{3}\pi {r^3}$ OR $\frac{{140}}{{100}} \times 288\pi = \frac{4}{3}\pi {r^3}$ OR $1266.69 \ldots = \frac{4}{3}\pi {r^3}$ (M1)(M1)

Note: Award (M1) for multiplying their part (a) by 1.4 or equivalent, (M1) for equating to the volume of a sphere formula.

${r^3} = \frac{{3 \times 1266.69 \ldots }}{{4\pi }}$ OR $r = \sqrt[3]{{\frac{{3 \times 1266.69 \ldots }}{{4\pi }}}}$ OR $r = \sqrt[3]{{(1.4) \times {6^3}}}$ OR ${r^3} = 302.4$ (M1)

Note: Award (M1) for isolating $r$ .

$(r = ){\text{ }}6.71{\text{ cm }}(6.71213 \ldots )$ (A1)(ft) (C4)

Note: Follow through from part (a).

[4 marks]

Examiners report

[N/A]

A cylindrical container with a radius of 8 cm is placed on a flat surface. The container is filled with water to a height of 12 cm, as shown in the following diagram.

M17/5/MATSD/SP1/ENG/TZ2/12

A heavy ball with a radius of 2.9 cm is dropped into the container. As a result, the height of the water increases to $h$ cm, as shown in the following diagram.

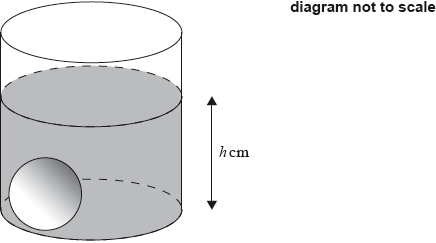
M17/5/MATSD/SP1/ENG/TZ2/12.b

Find the volume of water in the container.

[2]

Find the value of $h$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\pi \times {8^2} \times 12$ (M1)

Note: Award (M1) for correct substitution into the volume of a cylinder formula.

$2410{\text{ c}}{{\text{m}}^3}{\text{ }}(2412.74 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}768\pi {\text{ c}}{{\text{m}}^3})$ (A1) (C2)

[2 marks]

$\frac{4}{3}\pi \times {2.9^3} + 768\pi = \pi \times {8^2}h$ (M1)(M1)(M1)

Note: Award (M1) for correct substitution into the volume of a sphere formula (this may be implied by seeing 102.160…), (M1) for adding their volume of the ball to their part (a), (M1) for equating a volume to the volume of a cylinder with a height of $h$ .

$\frac{4}{3}\pi \times {2.9^3} = \pi \times {8^2}(h - 12)$ (M1)(M1)(M1)

Note: Award (M1) for correct substitution into the volume of a sphere formula (this may be implied by seeing 102.160…), (M1) for equating to the volume of a cylinder, (M1) for the height of the water level increase, $h - 12$ . Accept $h$ for $h - 12$ if adding 12 is implied by their answer.

$(h = ){\text{ }}12.5{\text{ (cm) }}\left( {12.5081 \ldots {\text{ (cm)}}} \right)$ (A1)(ft) (C4)

Note: If 3 sf answer used, answer is 12.5 (12.4944…). Follow through from part (a) if first method is used.

[4 marks]

Examiners report

[N/A]

Emily’s kite ABCD is hanging in a tree. The plane ABCDE is vertical.

Emily stands at point E at some distance from the tree, such that EAD is a straight line and angle BED = 7°. Emily knows BD = 1.2 metres and angle BDA = 53°, as shown in the diagram

N17/5/MATSD/SP1/ENG/TZ0/10

T is a point at the base of the tree. ET is a horizontal line. The angle of elevation of A from E is 41°.

Find the length of EB.

[3]

Write down the angle of elevation of B from E.

[1]

Find the vertical height of B above the ground.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

Units are required in parts (a) and (c).

$\frac{{{\text{EB}}}}{{\sin 53{\rm{^\circ }}}} = \frac{{1.2}}{{\sin 7{\rm{^\circ }}}}$ (M1)(A1)

Note: Award (M1) for substitution into sine formula, (A1) for correct substitution.

$({\text{EB}} = ){\text{ }}7.86{\text{ m}}$ $\,\,\,$ OR $\,\,\,$ $786{\text{ cm }}(7.86385 \ldots {\text{ m}}$ $\,\,\,$ OR $\,\,\,$ $786.385 \ldots {\text{ cm}})$ (A1) (C3)

[3 marks]

34° (A1) (C1)

[1 mark]

Units are required in parts (a) and (c).

$\sin 34^\circ = \frac{{{\text{height}}}}{{7.86385 \ldots }}$ (M1)

Note: Award (M1) for correct substitution into a trigonometric ratio.

$({\text{height}} = ){\text{ }}4.40{\text{ m}}$ $\,\,\,$ OR $\,\,\,$ $440{\text{ cm }}(4.39741 \ldots {\text{ m}}$ $\,\,\,$ OR $\,\,\,$ $439.741 \ldots {\text{ cm}})$ (A1)(ft) (C2)

Note: Accept “BT” used for height. Follow through from parts (a) and (b). Use of 7.86 gives an answer of 4.39525….

[2 marks]

Examiners report

[N/A]

The following diagram shows a right triangle ABC. Point D lies on AB such that CD bisects AĈB.

AĈD = θ and AC = 14 cm

Given that ${\text{sin}}\,\theta = \frac{3}{5}$ , find the value of ${\text{cos}}\,\theta$ .

[3]

Find the value of ${\text{cos}}\,2\theta$ .

[3]

Hence or otherwise, find ${\text{BC}}$ .

[2]

Markscheme

valid approach (M1)

eg labelled sides on separate triangle, ${\text{si}}{{\text{n}}^2}\,x + {\text{co}}{{\text{s}}^2}\,x = 1$

correct working (A1)

eg missing side is 4, $\sqrt {1 - {{\left( {\frac{3}{5}} \right)}^2}}$

${\text{cos}}\,\theta = \frac{4}{5}$ A1 N3

[3 marks]

correct substitution into ${\text{cos}}\,2\theta$ (A1)

eg $2\left( {\frac{{16}}{{25}}} \right) - 1$ , $1 - 2{\left( {\frac{3}{5}} \right)^2}$ , $\frac{{16}}{{25}} - \frac{9}{{25}}$

${\text{cos}}\,2\theta = \frac{7}{{25}}$ A1 N2

[2 marks]

correct working (A1)

eg $\frac{7}{{25}} = \frac{{14}}{{{\text{BC}}}}$ , ${\text{BC}} = \frac{{14 \times 25}}{7}$

${\text{BC}} = 50$ (cm) A1 N2

[2 marks]

Examiners report

[N/A]

A solid glass paperweight consists of a hemisphere of diameter 6 cm on top of a cuboid with a square base of length 6 cm, as shown in the diagram.

The height of the cuboid, x cm, is equal to the height of the hemisphere.

Write down the value of x.

[1]

a.i.

Calculate the volume of the paperweight.

[3]

a.ii.

1 cm³ of glass has a mass of 2.56 grams.

Calculate the mass, in grams, of the paperweight.

[2]

Markscheme

3 (cm) (A1) (C1)

[1 mark]

a.i.

units are required in part (a)(ii)

$\frac{1}{2} \times \frac{{4\pi \times {{\left( 3 \right)}^3}}}{3} + 3 \times {\left( 6 \right)^2}$ (M1)(M1)

Note: Award (M1) for their correct substitution in volume of sphere formula divided by 2, (M1) for adding their correctly substituted volume of the cuboid.

= 165 cm³(164.548…) (A1)(ft) (C3)

Note: The answer is 165 cm³; the units are required. Follow through from part (a)(i).

[3 marks]

a.ii.

their 164.548… × 2.56 (M1)

Note: Award (M1) for multiplying their part (a)(ii) by 2.56.

= 421 (g) (421.244…(g)) (A1)(ft) (C2)

Note: Follow through from part (a)(ii).

[2 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

A type of candy is packaged in a right circular cone that has volume ${\text{100 c}}{{\text{m}}^{\text{3}}}$ and vertical height 8 cm.

M17/5/MATSD/SP1/ENG/TZ1/09

Find the radius, $r$ , of the circular base of the cone.

[2]

Find the slant height, $l$ , of the cone.

[2]

Find the curved surface area of the cone.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$100 = \frac{1}{3}\pi {r^2}(8)$ (M1)

Note: Award (M1) for correct substitution into volume of cone formula.

$r = 3.45{\text{ (cm) }}\left( {3.45494 \ldots {\text{ (cm)}}} \right)$ (A1) (C2)

[2 marks]

${l^2} = {8^2} + {(3.45494 \ldots )^2}$ (M1)

Note: Award (M1) for correct substitution into Pythagoras’ theorem.

$l = 8.71{\text{ (cm) }}\left( {8.71416 \ldots {\text{ (cm)}}} \right)$ (A1)(ft) (C2)

Note: Follow through from part (a).

[2 marks]

$\pi \times 3.45494 \ldots \times 8.71416 \ldots$ (M1)

Note: Award (M1) for their correct substitutions into curved surface area of a cone formula.

$= 94.6{\text{ c}}{{\text{m}}^2}{\text{ }}(94.5836 \ldots {\text{ c}}{{\text{m}}^2})$ (A1)(ft) (C2)

Note: Follow through from parts (a) and (b). Accept $94.4{\text{ c}}{{\text{m}}^2}$ from use of 3 sf values.

[2 marks]

Examiners report

[N/A]

A solid right circular cone has a base radius of 21 cm and a slant height of 35 cm.
A smaller right circular cone has a height of 12 cm and a slant height of 15 cm, and is removed from the top of the larger cone, as shown in the diagram.

Calculate the radius of the base of the cone which has been removed.

[2]

Calculate the curved surface area of the cone which has been removed.

[2]

Calculate the curved surface area of the remaining solid.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\sqrt {{{15}^2} - {{12}^2}}$ (M1)

Note: Award (M1) for correct substitution into Pythagoras theorem.

$\frac{{{\text{radius}}}}{{21}} = \frac{{15}}{{35}}$ (M1)

Note: Award (M1) for a correct equation.

= 9 (cm) (A1) (C2)

[2 marks]

$\pi \times 9 \times 15$ (M1)

Note: Award (M1) for their correct substitution into curved surface area of a cone formula.

$= 424\,\,{\text{c}}{{\text{m}}^2}\,\,\,\,\,\left( {135\pi ,\,\,424.115...{\text{c}}{{\text{m}}^2}} \right)$ (A1)(ft) (C2)

Note: Follow through from part (a).

[2 marks]

$\pi \times 21 \times 35 - 424.115...$ (M1)

Note: Award (M1) for their correct substitution into curved surface area of a cone formula and for subtracting their part (b).

$= 1880\,\,{\text{c}}{{\text{m}}^2}\,\,\,\,\,\left( {600\pi ,\,\,1884.95...{\text{c}}{{\text{m}}^2}} \right)$ (A1)(ft) (C2)

Note: Follow through from part (b).

[2 marks]

Examiners report

[N/A]

The following diagram shows triangle ABC, with AB = 6 and AC = 8.

Given that ${\text{cos}}\,\hat A = \frac{5}{6}$ find the value of ${\text{sin}}\,\hat A$ .

[3]

Find the area of triangle ABC.

[2]

Markscheme

valid approach using Pythagorean identity (M1)

${\text{si}}{{\text{n}}^2}\,A + {\left( {\frac{5}{6}} \right)^2} = 1$ (or equivalent) (A1)

${\text{sin}}\,A = \frac{{\sqrt {11} }}{6}$ A1

[3 marks]

$\frac{1}{2} \times 8 \times 6 \times \frac{{\sqrt {11} }}{6}$ (or equivalent) (A1)

area $= 4\sqrt {11}$ A1

[2 marks]

Examiners report

[N/A]

A line $L$ passes through points ${\text{A}}( - 3,{\text{ }}4,{\text{ }}2)$ and ${\text{B}}( - 1,{\text{ }}3,{\text{ }}3)$ .

The line $L$ also passes through the point ${\text{C}}(3,{\text{ }}1,{\text{ }}p)$ .

Show that $\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right)$ .

[1]

a.i.

Find a vector equation for $L$ .

[2]

a.ii.

Find the value of $p$ .

[5]

The point D has coordinates $({q^2},{\text{ }}0,{\text{ }}q)$ . Given that $\overrightarrow {{\text{DC}}}$ is perpendicular to $L$ , find the possible values of $q$ .

[7]

Markscheme

correct approach A1

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \\ 3 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 3 \\ { - 4} \\ { - 2} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \\ 3 \end{array}} \right)$

$\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right)$ AG N0

[1 mark]

a.i.

any correct equation in the form $r = a + tb$ (any parameter for $t$ )

where $a$ is $\left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right)$ or $\left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \\ 3 \end{array}} \right)$ and $b$ is a scalar multiple of $\left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right)$ A2 N2

eg $\,\,\,\,\,$ $r = \left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right),{\text{ }}(x,{\text{ }}y,{\text{ }}z) = ( - 1,{\text{ }}3,{\text{ }}3) + s( - 2,{\text{ }}1,{\text{ }} - 1),{\text{ }}r = \left( {\begin{array}{*{20}{c}} { - 3 + 2t} \\ {4 - t} \\ {2 + t} \end{array}} \right)$

Note: Award A1 for the form $a + tb$ , A1 for the form $L = a + tb$ , A0 for the form $r = b + ta$ .

[2 marks]

a.ii.

METHOD 1 – finding value of parameter

valid approach (M1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right),{\text{ }}( - 1,{\text{ }}3,{\text{ }}3) + s( - 2,{\text{ }}1,{\text{ }} - 1) = (3,{\text{ }}1,{\text{ }}p)$

one correct equation (not involving $p$ ) (A1)

eg $\,\,\,\,\,$ $- 3 + 2t = 3,{\text{ }} - 1 - 2s = 3,{\text{ }}4 - t = 1,{\text{ }}3 + s = 1$

correct parameter from their equation (may be seen in substitution) A1

eg $\,\,\,\,\,$ $t = 3,{\text{ }}s = - 2$

correct substitution (A1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right) + 3\left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right),{\text{ }}3 - ( - 2)$

$p = 5\,\,\,\,\,\left( {{\text{accept }}\left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right)} \right)$ A1 N2

METHOD 2 – eliminating parameter

valid approach (M1)

one correct equation (not involving $p$ ) (A1)

eg $\,\,\,\,\,$ $- 3 + 2t = 3,{\text{ }} - 1 - 2s = 3,{\text{ }}4 - t = 1,{\text{ }}3 + s = 1$

correct equation (with $p$ ) A1

eg $\,\,\,\,\,$ $2 + t = p,{\text{ }}3 - s = p$

correct working to solve for $p$ (A1)

eg $\,\,\,\,\,$ $7 = 2p - 3,{\text{ }}6 = 1 + p$

$p = 5\,\,\,\,\,\left( {{\text{accept }}\left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right)} \right)$ A1 N2

[5 marks]

valid approach to find $\overrightarrow {{\text{DC}}}$ or $\overrightarrow {{\text{CD}}}$ (M1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{q^2}} \\ 0 \\ q \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{q^2}} \\ 0 \\ q \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ 5 \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{q^2}} \\ 0 \\ q \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3 \\ 1 \\ p \end{array}} \right)$

correct vector for $\overrightarrow {{\text{DC}}}$ or $\overrightarrow {{\text{CD}}}$ (may be seen in scalar product) A1

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} {3 - {q^2}} \\ 1 \\ {5 - q} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {{q^2} - 3} \\ { - 1} \\ {q - 5} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {3 - {q^2}} \\ 1 \\ {p - q} \end{array}} \right)$

recognizing scalar product of $\overrightarrow {{\text{DC}}}$ or $\overrightarrow {{\text{CD}}}$ with direction vector of $L$ is zero (seen anywhere) (M1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} {3 - {q^2}} \\ 1 \\ {p - q} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right) = 0,{\text{ }}\overrightarrow {{\text{DC}}} \bullet \overrightarrow {{\text{AC}}} = 0,{\text{ }}\left( {\begin{array}{*{20}{c}} {3 - {q^2}} \\ 1 \\ {5 - q} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 1 \end{array}} \right) = 0$

correct scalar product in terms of only $q$ A1

eg $\,\,\,\,\,$ $6 - 2{q^2} - 1 + 5 - q,{\text{ }}2{q^2} + q - 10 = 0,{\text{ }}2(3 - {q^2}) - 1 + 5 - q$

correct working to solve quadratic (A1)

eg $\,\,\,\,\,$ $(2q + 5)(q - 2),{\text{ }}\frac{{ - 1 \pm \sqrt {1 - 4(2)( - 10)} }}{{2(2)}}$

$q = - \frac{5}{2},{\text{ }}2$ A1A1 N3

[7 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

The position vectors of points P and Q are i $+$ 2 j $-$ k and 7i $+$ 3j $-$ 4k respectively.

Find a vector equation of the line that passes through P and Q.

[4]

The line through P and Q is perpendicular to the vector 2i $+$ nk. Find the value of $n$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid attempt to find direction vector (M1)

eg $\,\,\,\,\,$ $\overrightarrow {{\text{PQ}}} ,{\text{ }}\overrightarrow {{\text{QP}}}$

correct direction vector (or multiple of) (A1)

eg $\,\,\,\,\,$ 6i $+$ j $-$ 3k

any correct equation in the form r $=$ a $+$ tb (any parameter for $t$ ) A2 N3

where a is i $+$ 2j $-$ k or 7i $+$ 3j $-$ 4k , and b is a scalar multiple of 6i $+$ j $-$ 3k

eg $\,\,\,\,\,$ r $=$ 7i $+$ 3j $-$ 4k $+$ t(6i $+$ j $-$ 3k), r $= \left( {\begin{array}{*{20}{c}} {1 + 6s} \\ {2 + 1s} \\ { - 1 - 3s} \end{array}} \right),{\text{ }}r = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { - 1} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} { - 6} \\ { - 1} \\ 3 \end{array}} \right)$

Notes: Award A1 for the form a $+$ tb, A1 for the form L $=$ a $+$ tb, A0 for the form r $=$ b $+$ ta.

[4 marks]

correct expression for scalar product (A1)

eg $\,\,\,\,\,$ $6 \times 2 + 1 \times 0 + ( - 3) \times n,{\text{ }} - 3n + 12$

setting scalar product equal to zero (seen anywhere) (M1)

eg $\,\,\,\,\,$ u $\bullet$ v $= 0,{\text{ }} - 3n + 12 = 0$

$n = 4$ A1 N2

[3 marks]

Examiners report

[N/A]

Show that $2 x - 3 - \frac{6}{x - 1} = \frac{2 x^{2} - 5 x - 3}{x - 1}, x \in ℝ, x \neq 1$ .

[2]

Hence or otherwise, solve the equation $2 \sin 2 θ - 3 - \frac{6}{\sin 2 θ - 1} = 0$ for $0 \leq θ \leq π, θ \neq \frac{π}{4}$ .

[5]

Markscheme

METHOD 1

attempt to write all LHS terms with a common denominator of $x - 1$ (M1)

$2 x - 3 - \frac{6}{x - 1} = \frac{2 x (x - 1) - 3 (x - 1) - 6}{x - 1}$ OR $\frac{(2 x - 3) (x - 1)}{x - 1} - \frac{6}{x - 1}$

$= \frac{2 x^{2} - 2 x - 3 x + 3 - 6}{x - 1}$ OR $\frac{2 x^{2} - 5 x + 3}{x - 1} - \frac{6}{x - 1}$ A1

$= \frac{2 x^{2} - 5 x - 3}{x - 1}$ AG

METHOD 2

attempt to use algebraic division on RHS (M1)

correctly obtains quotient of $2 x - 3$ and remainder $- 6$ A1

$= 2 x - 3 - \frac{6}{x - 1}$ as required. AG

[2 marks]

consider the equation $\frac{2 \sin^{2} 2 θ - 5 \sin 2 θ - 3}{\sin 2 θ - 1} = 0$ (M1)

$\Rightarrow 2 \sin^{2} 2 θ - 5 \sin 2 θ - 3 = 0$

EITHER

attempt to factorise in the form $(2 \sin 2 θ + a) (\sin 2 θ + b)$ (M1)

Note: Accept any variable in place of $\sin 2 θ$ .

$(2 \sin 2 θ + 1) (\sin 2 θ - 3) = 0$

attempt to substitute into quadratic formula (M1)

$\sin 2 θ = \frac{5 \pm \sqrt{49}}{4}$

THEN

$\sin 2 θ = - \frac{1}{2}$ or $\sin 2 θ = 3$ (A1)

Note: Award A1 for $\sin 2 θ = - \frac{1}{2}$ only.

one of $\frac{7 π}{6}$ OR $\frac{11 π}{6}$ (accept $210$ or $330$ ) (A1)

$θ = \frac{7 π}{12}, \frac{11 π}{12}$ (must be in radians) A1

Note: Award A0 if additional answers given.

[5 marks]

Examiners report

[N/A]

A lampshade, in the shape of a cone, has a wireframe consisting of a circular ring and four straight pieces of equal length, attached to the ring at points A, B, C and D.

The ring has its centre at point O and its radius is 20 centimetres. The straight pieces meet at point V, which is vertically above O, and the angle they make with the base of the lampshade is 60°.

This information is shown in the following diagram.

M17/5/MATSD/SP1/ENG/TZ2/03

Find the length of one of the straight pieces in the wireframe.

[2]

Find the total length of wire needed to construct this wireframe. Give your answer in centimetres correct to the nearest millimetre.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\cos 60^\circ = \frac{{20}}{b}$ $\,\,\,$ OR $\,\,\,$ $b = \frac{{20}}{{\cos 60^\circ }}$ (M1)

Note: Award (M1) for correct substitution into a correct trig. ratio.

$(b = ){\text{ 40 (cm)}}$ (A1) (C2)

[2 marks]

$4 \times 40 + 2\pi (20)$ (M1)(M1)

Note: Award (M1) for correct substitution in the circumference of the circle formula, (M1) for adding 4 times their answer to part (a) to their circumference of the circle.

285.6637… (A1)(ft)

Note: Follow through from part (a). This (A1) may be implied by a correct rounded answer.

285.7 (cm) (A1)(ft) (C4)

Notes: Award (A1)(ft) for rounding their answer (consistent with their method) to the nearest millimetre, irrespective of unrounded answer seen.

The final (A1)(ft) is not dependent on any of the previous M marks. It is for rounding their unrounded answer correctly.

[4 marks]

Examiners report

[N/A]

Show that $\sin 2 x + \cos 2 x - 1 = 2 \sin x (\cos x - \sin x)$ .

[2]

Hence or otherwise, solve $\sin 2 x + \cos 2 x - 1 + \cos x - \sin x = 0$ for $0 < x < 2 π$ .

[6]

Markscheme

Note: Do not award the final A1 for proofs which work from both sides to find a common expression other than $2 \sin x \cos x - 2 \sin^{2} x$ .

METHOD 1 (LHS to RHS)

attempt to use double angle formula for $\sin 2 x$ or $\cos 2 x$ M1

LHS $= 2 \sin x \cos x + \cos 2 x - 1$ OR

$\sin 2 x + 1 - 2 \sin^{2} x - 1$ OR

$2 \sin x \cos x + 1 - 2 \sin^{2} x - 1$

$= 2 \sin x \cos x - 2 \sin^{2} x$ A1

$\sin 2 x + \cos 2 x - 1 = 2 \sin x (\cos x - \sin x) =$ RHS AG

METHOD 2 (RHS to LHS)

RHS $= 2 \sin x \cos x - 2 \sin^{2} x$

attempt to use double angle formula for $\sin 2 x$ or $\cos 2 x$ M1

$= \sin 2 x + 1 - 2 \sin^{2} x - 1$ A1

$= \sin 2 x + \cos 2 x - 1 =$ LHS AG

[2 marks]

attempt to factorise M1

$(\cos x - \sin x) (2 \sin x + 1) = 0$ A1

recognition of $\cos x = \sin x \Rightarrow \frac{\sin x}{\cos x} = \tan x = 1$ OR $\sin x = - \frac{1}{2}$ (M1)

one correct reference angle seen anywhere, accept degrees (A1)

$\frac{π}{4}$ OR $\frac{π}{6}$ (accept $- \frac{π}{6}, \frac{7 π}{6}$ )

Note: This (M1)(A1) is independent of the previous M1A1.

$x = \frac{7 π}{6}, \frac{11 π}{6}, \frac{π}{4}, \frac{5 π}{4}$ A2

Note: Award A1 for any two correct (radian) answers.
Award A1A0 if additional values given with the four correct (radian) answers.
Award A1A0 for four correct answers given in degrees.

[6 marks]

Examiners report

[N/A]

Three airport runways intersect to form a triangle, ABC. The length of AB is 3.1 km, AC is 2.6 km, and BC is 2.4 km.

A company is hired to cut the grass that grows in triangle ABC, but they need to know the area.

Find the size, in degrees, of angle BÂC.

[3]

Find the area, in km², of triangle ABC.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\left( {\cos \,A = } \right)\,\,\frac{{{{2.6}^2} + {{3.1}^2} - {{2.4}^2}}}{{2\left( {2.6} \right)\left( {3.1} \right)}}$ (M1)(A1)

Note: Award (M1) for substituted cosine rule formula, (A1) for correct substitutions.

48.8° (48.8381…°) (A1) (C3)

[3 marks]

$\frac{1}{2} \times 2.6 \times 3.1 \times {\text{sin}}\left( {48.8381 \ldots ^\circ } \right)$ (M1)(A1)(ft)

Note: Award (M1) for substituted area of a triangle formula, (A1) for correct substitution.

3.03 (km²) (3.033997…(km²)) (A1)(ft) (C3)

Note: Follow through from part (a).

[3 marks]

Examiners report

[N/A]

The following diagram shows a circle with centre O and radius r cm.

The points A and B lie on the circumference of the circle, and ${\text{A}}\mathop {\text{O}}\limits^ \wedge {\text{B}}$ = θ. The area of the shaded sector AOB is 12 cm² and the length of arc AB is 6 cm.

Find the value of r.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of correctly substituting into circle formula (may be seen later) A1A1
eg $\frac{1}{2}\theta {r^2} = 12,\,\,r\theta = 6$

attempt to eliminate one variable (M1)
eg $r = \frac{6}{\theta },\,\,\theta = \frac{1}{r},\,\,\frac{{\frac{1}{2}\theta {r^2}}}{{r\theta }} = \frac{{12}}{6}$

correct elimination (A1)
eg $\frac{1}{2} \times \frac{6}{r} \times {r^2} = 12,\,\,\frac{1}{2}\theta \times {\left( {\frac{6}{\theta }} \right)^2} = 12,\,\,A = \frac{1}{2} \times {r^2} \times \frac{l}{r},\,\,\frac{{{r^2}}}{{2r}} = 2$

correct equation (A1)
eg $\frac{1}{2} \times 6r = 12,\,\,\frac{1}{2} \times \frac{{36}}{\theta } = 12,\,\,12 = \frac{1}{2} \times {r^2} \times \frac{6}{r}$

correct working (A1)
eg $3r = 12,\,\,\frac{{18}}{\theta } = 12,\,\,\frac{r}{2} = 2,\,\,24 = 6r$

r = 4 (cm) A1 N2

[7 marks]

Examiners report

[N/A]

Solve ${\log _2}(2\sin x) + {\log _2}(\cos x) = - 1$ , for $2\pi < x < \frac{{5\pi }}{2}$ .

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct application of $\log a + \log b = \log ab$ (A1)

eg $\,\,\,\,\,$ ${\log _2}(2\sin x\cos x),{\text{ }}\log 2 + \log (\sin x) + \log (\cos x)$

correct equation without logs A1

eg $\,\,\,\,\,$ $2\sin x\cos x = {2^{ - 1}},{\text{ }}\sin x\cos x = \frac{1}{4},{\text{ }}\sin 2x = \frac{1}{2}$

recognizing double-angle identity (seen anywhere) A1

eg $\,\,\,\,\,$ $\log (\sin 2x),{\text{ }}2\sin x\cos x = \sin 2x,{\text{ }}\sin 2x = \frac{1}{2}$

evaluating ${\sin ^{ - 1}}\left( {\frac{1}{2}} \right) = \frac{\pi }{6}{\text{ }}(30^\circ )$ (A1)

correct working A1

eg $\,\,\,\,\,$ $x = \frac{\pi }{{12}} + 2\pi ,{\text{ }}2x = \frac{{25\pi }}{6},{\text{ }}\frac{{29\pi }}{6},{\text{ }}750^\circ ,{\text{ }}870^\circ ,{\text{ }}x = \frac{\pi }{{12}}$ and $x = \frac{{5\pi }}{{12}}$ , one correct final answer

$x = \frac{{25\pi }}{{12}},{\text{ }}\frac{{29\pi }}{{12}}$ (do not accept additional values) A2 N0

[7 marks]

Examiners report

[N/A]

The following diagram shows a ball attached to the end of a spring, which is suspended from a ceiling.

The height, $h$ metres, of the ball above the ground at time $t$ seconds after being released can be modelled by the function $h (t) = 0.4 \cos (π t) + 1.8$ where $t \geq 0$ .

Find the height of the ball above the ground when it is released.

[2]

Find the minimum height of the ball above the ground.

[2]

Show that the ball takes $2$ seconds to return to its initial height above the ground for the first time.

[2]

For the first 2 seconds of its motion, determine the amount of time that the ball is less than $1.8 + 0.2 \sqrt{2}$ metres above the ground.

[5]

Find the rate of change of the ball’s height above the ground when $t = \frac{1}{3}$ . Give your answer in the form $p π \sqrt{q} {ms}^{- 1}$ where $p \in ℚ$ and $q \in ℤ^{+}$ .

[4]

Markscheme

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

attempts to find $h (0)$ (M1)

$h (0) = 0.4 \cos (0) + 1.8 (= 2.2)$

$2.2$ (m) (above the ground) A1

[2 marks]

EITHER

uses the minimum value of $\cos (π t)$ which is $- 1$ M1

$0.4 (- 1) + 1.8$ (m)

the amplitude of motion is $0.4$ (m) and the mean position is $1.8$ (m) M1

finds $h' (t) = - 0.4 π \sin (π t)$ , attempts to solve $h' (t) = 0$ for $t$ and determines that the minimum height above the ground occurs at $t = 1, 3, \dots$ M1

$0.4 (- 1) + 1.8$ (m)

THEN

$1.4$ (m) (above the ground) A1

[2 marks]

EITHER

the ball is released from its maximum height and returns there a period later R1

the period is $\frac{2 π}{π} (= 2) (s)$ A1

attempts to solve $h (t) = 2.2$ for $t$ M1

$\cos (π t) = 1$

$t = 0, 2, \dots$ A1

THEN

so it takes $2$ seconds for the ball to return to its initial position for the first time AG

[2 marks]

$0.4 \cos (π t) + 1.8 = 1.8 + 0.2 \sqrt{2}$ (M1)

$0.4 \cos (π t) = 0.2 \sqrt{2}$

$\cos (π t) = \frac{\sqrt{2}}{2}$ A1

$π t = \frac{π}{4}, \frac{7 π}{4}$ (A1)

Note: Accept extra correct positive solutions for $π t$ .

$t = \frac{1}{4}, \frac{7}{4} (0 \leq t \leq 2)$ A1

Note: Do not award A1 if solutions outside $0 \leq t \leq 2$ are also stated.

the ball is less than $1.8 + 0.2 \sqrt{2}$ metres above the ground for $\frac{7}{4} - \frac{1}{4}$ (s)

$1.5$ (s) A1

[5 marks]

EITHER

attempts to find $h' (t)$ (M1)

recognizes that $h' (t)$ is required (M1)

THEN

$h' (t) = - 0.4 π \sin (π t)$ A1

attempts to evaluate their $h' (\frac{1}{3})$ (M1)

$h' (\frac{1}{3}) = - 0.4 π \sin \frac{π}{3}$

$= 0.2 π \sqrt{3} ({ms}^{- 1})$ A1

Note: Accept equivalent correct answer forms where $p \in ℚ$ . For example, $- \frac{1}{5} π \sqrt{3}$ .

[4 marks]

Examiners report

[N/A]

Iron in the asteroid 16 Psyche is said to be valued at $8973$ quadrillion euros $(EUR)$ , where one quadrillion $= 10^{15}$ .

James believes the asteroid is approximately spherical with radius $113 km$ . He uses this information to estimate its volume.

Write down the value of the iron in the form $a \times 10^{k}$ where $1 \leq a < 10, k \in ℤ$ .

[2]

Calculate James’s estimate of its volume, in ${km}^{3}$ .

[2]

The actual volume of the asteroid is found to be $6.074 \times 10^{6} {km}^{3}$ .

Find the percentage error in James’s estimate of the volume.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure. It appeared in a paper that permitted the use of a calculator, and so might not be suitable for all forms of practice.

$8.97 \times 10^{18} (EUR) (8.973 \times 10^{18})$ (A1)(A1) (C2)

Note: Award (A1) for $8.97 (8.973)$ , (A1) for $\times 10^{18}$ . Award (A1)(A0) for $8.97 E 18$ .
Award (A0)(A0) for answers of the type $8973 \times 10^{15}$ .

[2 marks]

$\frac{4 \times π \times 113^{3}}{3}$ (M1)

Note: Award (M1) for correct substitution in volume of sphere formula.

$6 040 000 ({km}^{3}) (6.04 \times 10^{6}, \frac{5771588 π}{3}, 6 043 992.82)$ (A1) (C2)

[2 marks]

$|\frac{6 043 992.82 - 6.074 \times 10^{6}}{6.074 \times 10^{6}}| \times 100$ (M1)

Note: Award (M1) for their correct substitution into the percentage error formula (accept a consistent absence of “ $\times 10^{6}$ ” from all terms).

$0.494 (%) (0.494026 \dots (%))$ (A1)(ft) (C2)

Note: Follow through from their answer to part (b). If the final answer is negative, award at most (M1)(A0).

[2 marks]

Examiners report

[N/A]

Consider the vectors a = $\left( {\begin{array}{*{20}{c}} 0 \\ 3 \\ p \end{array}} \right)$ and b = $\left( {\begin{array}{*{20}{c}} 0 \\ 6 \\ {18} \end{array}} \right)$ .

Find the value of $p$ for which a and b are

parallel.

[2]

perpendicular.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid approach (M1)

eg b = 2a, a = $k$ b, cos θ = 1, a•b = −|a||b|, 2 $p$ = 18

$p$ = 9 A1 N2

[2 marks]

evidence of scalar product (M1)

eg a•b, (0)(0) + (3)(6) + $p$ (18)

recognizing a•b = 0 (seen anywhere) (M1)

correct working (A1)

eg 18 + 18 $p$ = 0, 18 $p$ = −18 (A1)

$p$ = −1 A1 N3

[4 marks]

Examiners report

[N/A]

A cylinder with radius $r$ and height $h$ is shown in the following diagram.

The sum of $r$ and $h$ for this cylinder is 12 cm.

Write down an equation for the area, $A$ , of the curved surface in terms of $r$ .

[2]

Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .

[2]

Find the value of $r$ when the area of the curved surface is maximized.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$A = 2\pi r\left( {12 - r} \right)$ OR $A = 24\pi r - 2\pi {r^2}$ (A1)(M1) (C2)

Note: Award (A1) for $r + h = 12$ or $h = 12 - r$ seen. Award (M1) for correctly substituting into curved surface area of a cylinder. Accept $A = 2\pi r\left( {12 - r} \right)$ OR $A = 24\pi r - 2\pi {r^2}$ .

[2 marks]

$24\pi - 4\pi r$ (A1)(ft)(A1)(ft) (C2)

Note: Award (A1)(ft) for $24\pi$ and (A1)(ft) for $- 4\pi r$ . Follow through from part (a). Award at most (A1)(ft)(A0) if additional terms are seen.

[2 marks]

$24\pi - 4\pi r = 0$ (M1)

Note: Award (M1) for setting their part (b) equal to zero.

6 (cm) (A1)(ft) (C2)

Note: Follow through from part (b).

[2 marks]

Examiners report

[N/A]

Let $\theta$ be an obtuse angle such that ${\text{sin}}\,\theta = \frac{3}{5}$ .

Let $f\left( x \right) = {{\text{e}}^x}\,{\text{sin}}\,x - \frac{{3x}}{4}$ .

Find the value of ${\text{tan}}\,\theta$ .

[4]

Line $L$ passes through the origin and has a gradient of ${\text{tan}}\,\theta$ . Find the equation of $L$ .

[2]

The following diagram shows the graph of $f$ for 0 ≤ $x$ ≤ 3. Line $M$ is a tangent to the graph of $f$ at point P.

Given that $M$ is parallel to $L$ , find the $x$ -coordinate of P.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of valid approach (M1)

eg sketch of triangle with sides 3 and 5, ${\text{co}}{{\text{s}}^2}\,\theta = 1 - {\text{si}}{{\text{n}}^2}\,\theta$

correct working (A1)

eg missing side is 4 (may be seen in sketch), ${\text{cos}}\,\theta = \frac{4}{5}$ , ${\text{cos}}\,\theta = - \frac{4}{5}$

${\text{tan}}\,\theta = - \frac{3}{4}$ A2 N4

[4 marks]

correct substitution of either gradient or origin into equation of line (A1)

(do not accept $y = mx + b$ )

eg $y = x\,{\text{tan}}\,\theta$ , $y - 0 = m\left( {x - 0} \right)$ , $y = mx$

$y = - \frac{3}{4}x$ A2 N4

Note: Award A1A0 for $L = - \frac{3}{4}x$ .

[2 marks]

valid approach to equate their gradients (M1)

eg $f' = {\text{tan}}\,\theta$ , $f' = - \frac{3}{4}$ , ${{\text{e}}^x}\,{\text{cos}}\,x + {{\text{e}}^x}\,{\text{sin}}\,x - \frac{3}{4} = - \frac{3}{4}$ , ${{\text{e}}^x}\,\left( {{\text{cos}}\,x + {\text{sin}}\,x} \right) - \frac{3}{4} = - \frac{3}{4}$

correct equation without ${{\text{e}}^x}$ (A1)

eg ${\text{sin}}\,x = - {\text{cos}}\,x$ , ${\text{cos}}\,x + {\text{sin}}\,x = 0$ , $\frac{{ - {\text{sin}}\,x}}{{{\text{cos}}\,x}} = 1$

correct working (A1)

eg ${\text{tan}}\,\theta = - 1$ , $x = 135^\circ$

$x = \frac{{3\pi }}{4}$ (do not accept $135^\circ$ ) A1 N1

Note: Do not award the final A1 if additional answers are given.

[4 marks]

Examiners report

[N/A]

Consider $f (x) = 4 \sin x + 2.5$ and $g (x) = 4 \sin (x - \frac{3 π}{2}) + 2.5 + q$ , where $x \in ℝ$ and $q > 0$ .

The graph of $g$ is obtained by two transformations of the graph of $f$ .

Describe these two transformations.

[2]

The $y$ -intercept of the graph of $g$ is at $(0, r)$ .

Given that $g (x) \geq 7$ , find the smallest value of $r$ .

[5]

Markscheme

translation (shift) by $\frac{3 π}{2}$ to the right/positive horizontal direction A1

translation (shift) by $q$ upwards/positive vertical direction A1

Note: accept translation by $(\begin{matrix} \frac{3 π}{2} \\ q \end{matrix})$

Do not accept ‘move’ for translation/shift.

[2 marks]

METHOD 1

minimum of $4 \sin (x - \frac{3 π}{2})$ is $- 4$ (may be seen in sketch) (M1)

$- 4 + 2.5 + q \geq 7$

$q \geq 8.5$ (accept $q = 8.5$ ) A1

substituting $x = 0$ and their $q (= 8.5)$ to find $r$ (M1)

$(r =) 4 \sin (\frac{- 3 π}{2}) + 2.5 + 8.5$

$4 + 2.5 + 8.5$ (A1)

smallest value of $r$ is $15$ A1

METHOD 2

substituting $x = 0$ to find an expression (for $r$ ) in terms of $q$ (M1)

$(g (0) = r =) 4 \sin (\frac{- 3 π}{2}) + 2.5 + q$

$(r =) 6.5 + q$ A1

minimum of $4 \sin (x - \frac{3 π}{2})$ is $- 4$ (M1)

$- 4 + 2.5 + q \geq 7$

$- 4 + 2.5 + (r - 6.5) \geq 7$ (accept $=$ ) (A1)

smallest value of $r$ is $15$ A1

METHOD 3

$4 \sin (x - \frac{3 π}{2}) + 2.5 + q = 4 \cos x + 2.5 + q$ A1

$y$ -intercept of $4 \cos x + 2.5 + q$ is a maximum (M1)

amplitude of $g (x)$ is $4$ (A1)

attempt to find least maximum (M1)

$r = 2 \times 4 + 7$

smallest value of $r$ is $15$ A1

[5 marks]

Examiners report

Candidates knew aspects of the transformations performed but some were unable to correctly describe them fully, e.g., omitting direction (right/up/positive) or using 'move' instead of translate/shift. Each description requires three parts: transformation type, size and direction. e.g., translation of q units up. For part (b) few candidates were able to fully navigate the reasoning required in this question. A common error was to evaluate $\sin (\frac{- 3 π}{2}) = - 1$ , instead of 1. Those who used sketches to assist in their thinking were typically more successful.

[N/A]

Consider $f (x) = 4 \cos x (1 - 3 \cos 2 x + 3 \cos^{2} 2 x - \cos^{3} 2 x)$ .

Expand and simplify ${(1 - a)}^{3}$ in ascending powers of $a$ .

[2]

a.i.

By using a suitable substitution for $a$ , show that $1 - 3 \cos 2 x + 3 \cos^{2} 2 x - \cos^{3} 2 x = 8 \sin^{6} x$ .

[4]

a.ii.

Show that $\int_{0}^{m} f (x) d x = \frac{32}{7} \sin^{7} m$ , where $m$ is a positive real constant.

[4]

b.i.

It is given that $\int_{m}^{\frac{π}{2}} f (x) d x = \frac{127}{28}$ , where $0 \leq m \leq \frac{π}{2}$ . Find the value of $m$ .

[5]

b.ii.

Markscheme

EITHER

attempt to use binomial expansion (M1)

$1 + {}_{3}C_{1} \times 1 \times (- a) + {}_{3}C_{2} \times 1 \times {(- a)}^{2} + 1 \times {(- a)}^{3}$

$(1 - a) (1 - a) (1 - a)$

$= (1 - a) (1 - 2 a + a^{2})$ (M1)

THEN

$= 1 - 3 a + 3 a^{2} - a^{3}$ A1

[2 marks]

a.i.

$a = \cos 2 x$ (A1)

So, $1 - 3 \cos 2 x + 3 \cos^{2} 2 x - \cos^{3} 2 x =$

${(1 - \cos 2 x)}^{3}$ A1

attempt to substitute any double angle rule for $\cos 2 x$ into ${(1 - \cos 2 x)}^{3}$ (M1)

$= {(2 \sin^{2} x)}^{3}$ A1

$= 8 \sin^{6} x$ AG

Note: Allow working RHS to LHS.

[4 marks]

a.ii.

recognizing to integrate $\int (4 \cos x \times 8 \sin^{6} x) d x$ (M1)

EITHER

applies integration by inspection (M1)

$32 \int (\cos x \times {(\sin x)}^{6}) d x$

$= \frac{32}{7} \sin^{7} x (+ c)$ A1

${[\frac{32}{7} \sin^{7} x]}_{0}^{m} (= \frac{32}{7} \sin^{7} m - \frac{32}{7} \sin^{7} 0)$ A1

$u = \sin x \Rightarrow \frac{d u}{d x} = \cos x$ (M1)

$\int 32 \cos x (\sin^{6} x) d x = \int 32 u^{6} d u$

$= \frac{32}{7} u^{7} (+ c)$ A1

${[\frac{32}{7} \sin^{7} x]}_{0}^{m}$ OR ${[\frac{32}{7} u^{7}]}_{0}^{\sin m} (= \frac{32}{7} \sin^{7} m - \frac{32}{7} \sin^{7} 0)$ A1

THEN

$= \frac{32}{7} \sin^{7} m$ AG

[4 marks]

b.i.

EITHER

$\int_{m}^{\frac{π}{2}} f (x) d x (= {[\frac{32}{7} \sin^{7} x]}_{m}^{\frac{π}{2}}) = \frac{32}{7} \sin^{7} \frac{π}{2} - \frac{32}{7} \sin^{7} m$ M1

$\frac{32}{7} \sin^{7} \frac{π}{2} - \frac{32}{7} \sin^{7} m = \frac{127}{28}$ OR $\frac{32}{7} (1 - \sin^{7} m) = \frac{127}{28}$ (M1)

$\int_{0}^{\frac{π}{2}} f (x) d x = \int_{0}^{m} f (x) d x + \int_{m}^{\frac{π}{2}} f (x) d x$ M1

$\frac{32}{7} = \frac{32}{7} \sin^{7} m + \frac{127}{28}$ (M1)

THEN

$\sin^{7} m = \frac{1}{128} (= \frac{1}{2^{7}})$ (A1)

$\sin m = \frac{1}{2}$ (A1)

$m = \frac{π}{6}$ A1

[5 marks]

b.ii.

Examiners report

Many candidates successfully expanded the binomial, with the most common error being to omit the negative sign with a. The connection between (a)(i) and (ii) was often noted but not fully utilised with candidates embarking on unnecessary complex algebraic expansions of expressions involving double angle rules. Candidates often struggled to apply inspection or substitution when integrating. As a 'show that' question, b(i) provided a useful result to be utilised in (ii). So even without successfully completing (i) candidates could apply it in part (ii). Not many managed to do so.

a.i.

[N/A]

a.ii.

[N/A]

b.i.

[N/A]

b.ii.

AC is a vertical communications tower with its base at C.

The tower has an observation deck, D, three quarters of the way to the top of the tower, A.

N16/5/MATSD/SP1/ENG/TZ0/11

From a point B, on horizontal ground 250 m from C, the angle of elevation of D is 48°.

Calculate CD, the height of the observation deck above the ground.

[2]

Calculate the angle of depression from A to B.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\tan 48^\circ = \frac{{{\text{CD}}}}{{250}}$ (M1)

Note: Award (M1) for correct substitution into the tangent ratio.

$({\text{CD}} = ){\text{ }}278{\text{ }}({\text{m}}){\text{ }}(277.653 \ldots )$ (A1) (C2)

[2 marks]

$\tan {\text{ABC (or equivalent)}} = \frac{{\frac{4}{3} \times 277.653 \ldots }}{{250}}$ (M1)(M1)(M1)

Note: Award (M1) for $\frac{4}{3}$ multiplying their part (a), (M1) for substitution into the tangent ratio, (M1) for correct substitution.

$90 - {\tan ^{ - 1}}\left( {\frac{{250}}{{\frac{4}{3} \times 277.653 \ldots }}} \right)$ (M1)(M1)(M1)

Note: Award (M1) for $\frac{4}{3}$ multiplying their part (a), (M1) for substitution into the tangent ratio, (M1) for subtracting from 90 and for correct substitution.

${\text{(angle of depression}} = {\text{) }}56.0^\circ {\text{ }}(55.9687 \ldots )$ (A1)(ft) (C4)

Note: Follow through from part (a).

[4 marks]

Examiners report

[N/A]

Points $A$ and $B$ have coordinates $(1, 1, 2)$ and $(9, m, - 6)$ respectively.

The line $L$ , which passes through $B$ , has equation $r = (\begin{matrix} - 3 \\ - 19 \\ 24 \end{matrix}) + s (\begin{matrix} 2 \\ 4 \\ - 5 \end{matrix})$ .

Express $\vec{AB}$ in terms of $m$ .

[2]

Find the value of $m$ .

[5]

Consider a unit vector $u$ , such that $u = p i - \frac{2}{3} j + \frac{1}{3} k$ , where $p > 0$ .

Point $C$ is such that $\vec{BC} = 9 u$ .

Find the coordinates of $C$ .

[8]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid approach to find $\vec{AB}$ (M1)

eg $\vec{OB} - \vec{OA}, A - B$

$\vec{AB} = (\begin{matrix} 8 \\ m - 1 \\ - 8 \end{matrix})$ A1 N2

[2 marks]

valid approach (M1)

eg $L = (\begin{matrix} 9 \\ m \\ - 6 \end{matrix}), (\begin{matrix} 9 \\ m \\ - 6 \end{matrix}) = (\begin{matrix} - 3 \\ - 19 \\ 24 \end{matrix}) + s (\begin{matrix} 2 \\ 4 \\ - 5 \end{matrix})$

one correct equation (A1)

eg $- 3 + 2 s = 9, - 6 = 24 - 5 s$

correct value for $s$ A1

eg $s = 6$

substituting their $s$ value into their expression/equation to find $m$ (M1)

eg $- 19 + 6 \times 4$

$m = 5$ A1 N3

[5 marks]

valid approach (M1)

eg $\vec{BC} = (\begin{matrix} 9 p \\ - 6 \\ 3 \end{matrix}), C = 9 u + B, \vec{BC} = (\begin{matrix} x - 9 \\ y - 5 \\ z + 6 \end{matrix})$

correct working to find $C$ (A1)

eg $\vec{OC} = (\begin{matrix} 9 p + 9 \\ - 1 \\ - 3 \end{matrix}), C = 9 (\begin{matrix} p \\ - \frac{2}{3} \\ \frac{1}{3} \end{matrix}) + (\begin{matrix} 9 \\ 5 \\ - 6 \end{matrix}), y = - 1$ and $z = - 3$

correct approach to find $|u|$ (seen anywhere) A1

eg $p^{2} + {(- \frac{2}{3})}^{2} + {(\frac{1}{3})}^{2}, \sqrt{p^{2} + \frac{4}{9} + \frac{1}{9}}$

recognizing unit vector has magnitude of $1$ (M1)

eg $|u| = 1, \sqrt{p^{2} + {(- \frac{2}{3})}^{2} + {(\frac{1}{3})}^{2}} = 1, p^{2} + \frac{5}{9} = 1$

correct working (A1)

eg $p^{2} = \frac{4}{9}, p = \pm \frac{2}{3}$

$p = \frac{2}{3}$ A1

substituting their value of $p$ (M1)

eg $(\begin{matrix} x - 9 \\ y - 5 \\ z + 6 \end{matrix}) = (\begin{matrix} 6 \\ - 6 \\ 3 \end{matrix}), C = (\begin{matrix} 6 \\ - 6 \\ 3 \end{matrix}) + (\begin{matrix} 9 \\ 5 \\ - 6 \end{matrix}), C = 9 (\begin{matrix} \frac{2}{3} \\ - \frac{2}{3} \\ \frac{1}{3} \end{matrix}) + (\begin{matrix} 9 \\ 5 \\ - 6 \end{matrix}), x - 9 = 6$

$C (15, - 1, - 3)$ (accept $(\begin{matrix} 15 \\ - 1 \\ - 3 \end{matrix})$ ) A1 N4

Note: The marks for finding $p$ are independent of the first two marks.
For example, it is possible to award marks such as (M0)(A0)A1(M1)(A1)A1 (M0)A0 or (M0)(A0)A1(M1)(A0)A0 (M1)A0.

[8 marks]

Examiners report

[N/A]

Show that the equation $2 \cos^{2} x + 5 \sin x = 4$ may be written in the form $2 \sin^{2} x - 5 \sin x + 2 = 0$ .

[1]

Hence, solve the equation $2 \cos^{2} x + 5 \sin x = 4, 0 \leq x \leq 2 π$ .

[5]

Markscheme

METHOD 1

correct substitution of $\cos^{2} x = 1 - \sin^{2} x$ A1

$2 (1 - \sin^{2} x) + 5 \sin x = 4$

$2 \sin^{2} x - 5 \sin x + 2 = 0$ AG

METHOD 2

correct substitution using double-angle identities A1

$(2 \cos^{2} x - 1) + 5 \sin x = 3$

$1 - 2 \sin^{2} x - 5 \sin x = 3$

$2 \sin^{2} x - 5 \sin x + 2 = 0$ AG

[1 mark]

EITHER

attempting to factorise M1

$(2 \sin x - 1) (\sin x - 2)$ A1

attempting to use the quadratic formula M1

$\sin x = \frac{5 \pm \sqrt{5^{2} - 4 \times 2 \times 2}}{4} (= \frac{5 \pm 3}{4})$ A1

THEN

$\sin x = \frac{1}{2}$ (A1)

$x = \frac{π}{6}, \frac{5 π}{6}$ A1A1

[5 marks]

Examiners report

[N/A]

The following diagram shows triangle $ABC$ , with $AB = 10$ , $BC = x$ and $AC = 2 x$ .

Given that $\cos \hat{C} = \frac{3}{4}$ , find the area of the triangle.

Give your answer in the form $\frac{p \sqrt{q}}{2}$ where $p, q \in ℤ^{+}$ .

Markscheme

METHOD 1

attempt to use the cosine rule to find the value of $x$ (M1)

$100 = x^{2} + 4 x^{2} - 2 (x) (2 x) (\frac{3}{4})$ A1

$2 x^{2} = 100$

$x^{2} = 50$ OR $x = \sqrt{50} (= 5 \sqrt{2})$ A1

attempt to find $\sin \hat{C}$ (seen anywhere) (M1)

$\sin^{2} \hat{C} + {(\frac{3}{4})}^{2} = 1$ OR $x^{2} + 3^{2} = 4^{2}$ or right triangle with side $3$ and hypotenuse $4$

$\sin \hat{C} = \frac{\sqrt{7}}{4}$ (A1)

Note: The marks for finding $\sin \hat{C}$ may be awarded independently of the first three marks for finding $x$ .

correct substitution into the area formula using their value of $x$ (or $x^{2}$ ) and their value of $\sin \hat{C}$ (M1)

$A = \frac{1}{2} \times 5 \sqrt{2} \times 10 \sqrt{2} \times \frac{\sqrt{7}}{4}$ or $A = \frac{1}{2} \times \sqrt{50} \times 2 \sqrt{50} \times \frac{\sqrt{7}}{4}$

$A = \frac{25 \sqrt{7}}{2}$ A1

METHOD 2

attempt to find the height, $h$ , of the triangle in terms of $x$ (M1)

$h^{2} + {(\frac{3}{4} x)}^{2} = x^{2}$ OR $h^{2} + {(\frac{5}{4} x)}^{2} = 10^{2}$ OR $h = \frac{\sqrt{7}}{4} x$ A1

equating their expressions for either $h^{2}$ or $h$ (M1)

$x^{2} - {(\frac{3}{4} x)}^{2} = 10^{2} - {(\frac{5}{4} x)}^{2}$ OR $\sqrt{100 - \frac{25}{16} x^{2}} = \frac{\sqrt{7}}{4} x$ (or equivalent) A1

$x^{2} = 50$ OR $x = \sqrt{50} (= 5 \sqrt{2})$ A1

correct substitution into the area formula using their value of $x$ (or $x^{2}$ ) (M1)

$A = \frac{1}{2} \times 2 \sqrt{50} \times \frac{\sqrt{7}}{4} \sqrt{50}$ OR $A = \frac{1}{2} (2 \times 5 \sqrt{2}) (\frac{\sqrt{7}}{4} 5 \sqrt{2})$

$A = \frac{25 \sqrt{7}}{2}$ A1

[7 marks]

Examiners report

[N/A]

Find the least positive value of $x$ for which $\cos (\frac{x}{2} + \frac{π}{3}) = \frac{1}{\sqrt{2}}$ .

Markscheme

determines $\frac{π}{4}$ (or $45 °$ ) as the first quadrant (reference) angle (A1)

attempts to solve $\frac{x}{2} + \frac{π}{3} = \frac{π}{4}$ (M1)

Note: Award M1 for attempting to solve $\frac{x}{2} + \frac{π}{3} = \frac{π}{4}, \frac{7 π}{4} (, \dots)$

$\frac{x}{2} + \frac{π}{3} = \frac{π}{4} \Rightarrow x < 0$ and so $\frac{π}{4}$ is rejected (R1)

$\frac{x}{2} + \frac{π}{3} = 2 π - \frac{π}{4} (= \frac{7 π}{4})$ A1

$x = \frac{17 π}{6}$ (must be in radians) A1

[5 marks]

Examiners report

This question proved to be a struggle for many candidates, and some candidates made no attempt here. While a good number of candidates recognized the reference angle of $\frac{π}{4}$ , this led to a final answer of $x = - \frac{π}{6}$ , which many left as their final answer. In other cases, some candidates heeded the requirement that $x$ must be a positive value, however they gave an incorrect final answer of $x = \frac{11 π}{6}$ . Few candidates correctly rejected their initial reference angle of $\frac{π}{4}$ and correctly solved an equation using $\frac{x}{2} + \frac{π}{3} = \frac{7 π}{4}$ .

In this question, all lengths are in metres and time is in seconds.

Consider two particles, $P_{1}$ and $P_{2}$ , which start to move at the same time.

Particle $P_{1}$ moves in a straight line such that its displacement from a fixed-point is given by $s (t) = 10 - \frac{7}{4} t^{2}$ , for $t \geq 0$ .

Find an expression for the velocity of $P_{1}$ at time $t$ .

[2]

Particle $P_{2}$ also moves in a straight line. The position of $P_{2}$ is given by $r = (\begin{matrix} - 1 \\ 6 \end{matrix}) + t (\begin{matrix} 4 \\ - 3 \end{matrix})$ .

The speed of $P_{1}$ is greater than the speed of $P_{2}$ when $t > q$ .

Find the value of $q$ .

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

recognizing velocity is derivative of displacement (M1)

eg $v = \frac{d s}{d t}, \frac{d}{d t} (10 - \frac{7}{4} t^{2})$

velocity $= - \frac{14}{4} t (= - \frac{7}{2} t)$ A1 N2

[2 marks]

valid approach to find speed of $P_{2}$ (M1)

eg $|(\begin{matrix} 4 \\ - 3 \end{matrix})|, \sqrt{4^{2} + {(- 3)}^{2}}$ , velocity $= \sqrt{4^{2} + {(- 3)}^{2}}$

correct speed (A1)

eg $5 {m s}^{- 1}$

recognizing relationship between speed and velocity (may be seen in inequality/equation) R1

eg $|- \frac{7}{2} t|$ , speed = | velocity | , graph of $P_{1}$ speed , $P_{1}$ speed $= \frac{7}{2} t, P_{2}$ velocity $= - 5$

correct inequality or equation that compares speed or velocity (accept any variable for $q$ ) A1

eg $|- \frac{7}{2} t| > 5, - \frac{7}{2} q < - 5, \frac{7}{2} q > 5, \frac{7}{2} q = 5$

$q = \frac{10}{7}$ (seconds) (accept $t > \frac{10}{7}$ , do not accept $t = \frac{10}{7}$ ) A1 N2

Note: Do not award the last two A1 marks without the R1.

[5 marks]

Examiners report

[N/A]

Let $\sin \theta = \frac{{\sqrt 5 }}{3}$ , where $\theta$ is acute.

Find $\cos \theta$ .

[3]

Find $\cos 2\theta$ .

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of valid approach (M1)

eg $\,\,\,\,\,$ right triangle, ${\cos ^2}\theta = 1 - {\sin ^2}\theta$

correct working (A1)

eg $\,\,\,\,\,$ missing side is 2, $\sqrt {1 - {{\left( {\frac{{\sqrt 5 }}{3}} \right)}^2}}$

$\cos \theta = \frac{2}{3}$ A1 N2

[3 marks]

correct substitution into formula for $\cos 2\theta$ (A1)

eg $\,\,\,\,\,$ $2 \times {\left( {\frac{2}{3}} \right)^2} - 1,{\text{ }}1 - 2{\left( {\frac{{\sqrt 5 }}{3}} \right)^2},{\text{ }}{\left( {\frac{2}{3}} \right)^2} - {\left( {\frac{{\sqrt 5 }}{3}} \right)^2}$

$\cos 2\theta = - \frac{1}{9}$ A1 N2

[2 marks]

Examiners report

[N/A]

A triangular postage stamp, ABC, is shown in the diagram below, such that ${\text{AB}} = 5{\text{ cm}},{\rm{ B\hat AC}} = 34^\circ ,{\rm{ A\hat BC}} = 26^\circ$ and ${\rm{A\hat CB}} = 120^\circ$ .

M17/5/MATSD/SP1/ENG/TZ1/13

Find the length of BC.

[3]

Find the area of the postage stamp.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{{{\text{BC}}}}{{\sin 34^\circ }} = \frac{5}{{\sin 120^\circ }}$ (M1)(A1)

Note: Award (M1) for substituted sine rule formula, (A1) for correct substitutions.

${\text{BC}} = 3.23{\text{ (cm) }}\left( {3.22850 \ldots {\text{ (cm)}}} \right)$ (A1) (C3)

[3 marks]

$\frac{1}{2}(5)(3.22850)\sin 26^\circ$ (M1)(A1)(ft)

Note: Award (M1) for substituted area of a triangle formula, (A1) for correct substitutions.

$= 3.54{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}\left( {3.53820 \ldots {\text{ }}({\text{c}}{{\text{m}}^2})} \right)$ (A1)(ft) (C3)

Note: Follow through from part (a).

[3 marks]

Examiners report

[N/A]

The following diagram shows triangle ABC, with ${\text{AB}} = 3{\text{ cm}}$ , ${\text{BC}} = 8{\text{ cm}}$ , and ${\rm{A\hat BC = }}\frac{\pi }{3}$ .

N17/5/MATME/SP1/ENG/TZ0/04

Show that ${\text{AC}} = 7{\text{ cm}}$ .

[4]

The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

N17/5/MATME/SP1/ENG/TZ0/04.b

Find the exact perimeter of this shape.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of choosing the cosine rule (M1)

eg $\,\,\,\,\,$ ${c^2} = {a^2} + {b^2} - ab\cos C$

correct substitution into RHS of cosine rule (A1)

eg $\,\,\,\,\,$ ${3^2} + {8^2} - 2 \times 3 \times 8 \times \cos \frac{\pi }{3}$

evidence of correct value for $\cos \frac{\pi }{3}$ (may be seen anywhere, including in cosine rule) A1

eg $\,\,\,\,\,$ $\cos \frac{\pi }{3} = \frac{1}{2},{\text{ A}}{{\text{C}}^2} = 9 + 64 - \left( {48 \times \frac{1}{2}} \right),{\text{ }}9 + 64 - 24$

correct working clearly leading to answer A1

eg $\,\,\,\,\,$ ${\text{A}}{{\text{C}}^2} = 49,{\text{ }}b = \sqrt {49}$

${\text{AC}} = 7{\text{ (cm)}}$ AG N0

Note: Award no marks if the only working seen is ${\text{A}}{{\text{C}}^2} = 49$ or ${\text{AC}} = \sqrt {49}$ (or similar).

[4 marks]

correct substitution for semicircle (A1)

eg $\,\,\,\,\,$ ${\text{semicircle}} = \frac{1}{2}(2\pi \times 3.5),{\text{ }}\frac{1}{2} \times \pi \times 7,{\text{ }}3.5\pi$

valid approach (seen anywhere) (M1)

eg $\,\,\,\,\,$ ${\text{perimeter}} = {\text{AB}} + {\text{BC}} + {\text{semicircle, }}3 + 8 + \left( {\frac{1}{2} \times 2 \times \pi \times \frac{7}{2}} \right),{\text{ }}8 + 3 + 3.5\pi$

$11 + \frac{7}{2}\pi {\text{ }}( = 3.5\pi + 11){\text{ (cm)}}$ A1 N2

[3 marks]

Examiners report

[N/A]

Six equilateral triangles, each with side length 3 cm, are arranged to form a hexagon.
This is shown in the following diagram.

The vectors p , q and r are shown on the diagram.

Find p•(p + q + r).

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1 (using |p| |2q| cosθ)

finding p + q + r (A1)

eg 2q,

| p + q + r | = 2 × 3 (= 6) (seen anywhere) A1

correct angle between p and q (seen anywhere) (A1)

$\frac{\pi }{3}$ (accept 60°)

substitution of their values (M1)

eg 3 × 6 × cos $\left( {\frac{\pi }{3}} \right)$

correct value for cos $\left( {\frac{\pi }{3}} \right)$ (seen anywhere) (A1)

eg $\frac{1}{2},\,\,\,3 \times 6 \times \frac{1}{2}$

p•(p + q + r) = 9 A1 N3

METHOD 2 (scalar product using distributive law)

correct expression for scalar distribution (A1)

eg p• p + p•q + p•r

three correct angles between the vector pairs (seen anywhere) (A2)

eg 0° between p and p, $\frac{\pi }{3}$ between p and q, $\frac{{2\pi }}{3}$ between p and r

Note: Award A1 for only two correct angles.

substitution of their values (M1)

eg 3.3.cos0 +3.3.cos $\frac{\pi }{3}$ + 3.3.cos120

one correct value for cos0, cos $\left( {\frac{\pi }{3}} \right)$ or cos $\left( {\frac{2\pi }{3}} \right)$ (seen anywhere) A1

eg $\frac{1}{2},\,\,\,3 \times 6 \times \frac{1}{2}$

p•(p + q + r) = 9 A1 N3

METHOD 3 (scalar product using relative position vectors)

valid attempt to find one component of p or r (M1)

eg sin 60 = $\frac{x}{3}$ , cos 60 = $\frac{x}{3}$ , one correct value $\frac{3}{2},\,\,\frac{{3\sqrt 3 }}{2},\,\,\frac{{ - 3\sqrt 3 }}{2}$

one correct vector (two or three dimensions) (seen anywhere) A1

eg $p = \left( \begin{gathered} \,\,\,\frac{3}{2} \hfill \\ \frac{{3\sqrt 3 }}{2} \hfill \\ \end{gathered} \right),\,\,q = \left( \begin{gathered} 3 \hfill \\ 0 \hfill \\ \end{gathered} \right),\,\,r = \left( \begin{gathered} \,\,\,\,\frac{3}{2} \hfill \\ - \frac{{3\sqrt 3 }}{2} \hfill \\ \,\,\,\,0 \hfill \\ \end{gathered} \right)$

three correct vectors p + q + r = 2q (A1)

p + q + r = $\left( \begin{gathered} 6 \hfill \\ 0 \hfill \\ \end{gathered} \right)$ or $\left( \begin{gathered} 6 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right)$ (seen anywhere, including scalar product) (A1)

correct working (A1)
eg $\left( {\frac{3}{2} \times 6} \right) + \left( {\frac{{3\sqrt 3 }}{2} \times 0} \right),\,\,9 + 0 + 0$

p•(p + q + r) = 9 A1 N3

[6 marks]

Examiners report

[N/A]

Point A has coordinates (−4, −12, 1) and point B has coordinates (2, −4, −4).

The line L passes through A and B.

Show that $\mathop {{\text{AB}}}\limits^ \to = \left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right)$

[1]

Find a vector equation for L.

[2]

b.i.

Point C (k , 12 , −k) is on L. Show that k = 14.

[4]

b.ii.

Find $\mathop {{\text{OB}}}\limits^ \to \, \bullet \mathop {{\text{AB}}}\limits^ \to$ .

[2]

c.i.

Write down the value of angle OBA.

[1]

c.ii.

Point D is also on L and has coordinates (8, 4, −9).

Find the area of triangle OCD.

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct approach A1

eg $\mathop {{\text{AO}}}\limits^ \to \,\, + \,\,\mathop {{\text{OB}}}\limits^ \to ,\,\,\,{\text{B}} - {\text{A}}\,{\text{, }}\,\left( \begin{gathered} \,\,2 \hfill \\ - 4 \hfill \\ - 4 \hfill \\ \end{gathered} \right) - \left( \begin{gathered} \, - 4 \hfill \\ - 12 \hfill \\ \,\,\,1 \hfill \\ \end{gathered} \right)$

$\mathop {{\text{AB}}}\limits^ \to = \left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right)$ AG N0

[1 mark]

any correct equation in the form r = a + tb (any parameter for t) A2 N2

where a is $\left( \begin{gathered} \,\,2 \hfill \\ - 4 \hfill \\ - 4 \hfill \\ \end{gathered} \right)$ or $\left( \begin{gathered} \, - 4 \hfill \\ - 12 \hfill \\ \,\,\,1 \hfill \\ \end{gathered} \right)$ and b is a scalar multiple of $\left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right)$

eg r $= \left( \begin{gathered} \, - 4 \hfill \\ - 12 \hfill \\ \,\,\,1 \hfill \\ \end{gathered} \right) + t\left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right),\,\,\left( {x,\,\,y,\,\,z} \right) = \left( {2,\,\, - 4,\,\, - 4} \right) + t\left( {6,\,\,8,\,\, - 5} \right),$ r $= \left( \begin{gathered} \, - 4 + 6t \hfill \\ - 12 + 8t \hfill \\ \,\,\,1 - 5t \hfill \\ \end{gathered} \right)$

Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.

[2 marks]

b.i.

METHOD 1 (solving for t)

valid approach (M1)

eg $\left( \begin{gathered} \,k \hfill \\ 12 \hfill \\ - k \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \,\,2 \hfill \\ - 4 \hfill \\ - 4 \hfill \\ \end{gathered} \right) + t\left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right),\,\,\left( \begin{gathered} \,k \hfill \\ 12 \hfill \\ - k \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \, - 4 \hfill \\ - 12 \hfill \\ \,\,\,1 \hfill \\ \end{gathered} \right) + t\left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right)$

one correct equation A1

eg −4 + 8t = 12, −12 + 8t = 12

correct value for t (A1)

eg t = 2 or 3

correct substitution A1

eg 2 + 6(2), −4 + 6(3), −[1 + 3(−5)]

k = 14 AG N0

METHOD 2 (solving simultaneously)

valid approach (M1)

two correct equations in A1

eg k = −4 + 6t, −k = 1 −5t

EITHER (eliminating k)

correct value for t (A1)

eg t = 2 or 3

correct substitution A1

eg 2 + 6(2), −4 + 6(3)

OR (eliminating t)

correct equation(s) (A1)

eg 5k + 20 = 30t and −6k − 6 = 30t, −k = 1 − 5 $\left( {\frac{{k + 4}}{6}} \right)$

correct working clearly leading to k = 14 A1

eg −k + 14 = 0, −6k = 6 −5k − 20, 5k = −20 + 6(1 + k)

THEN

k = 14 AG N0

[4 marks]

b.ii.

correct substitution into scalar product A1

eg (2)(6) − (4)(8) − (4)(−5), 12 − 32 + 20

$\mathop {{\text{OB}}}\limits^ \to \, \bullet \mathop {{\text{AB}}}\limits^ \to$ = 0 A1 N0

[2 marks]

c.i.

${\text{O}}\mathop {\text{B}}\limits^ \wedge {\text{A}} = \frac{\pi }{2},\,\,90^\circ \,\,\,\,\,\left( {{\text{accept}}\,\frac{{3\pi }}{2},\,\,270^\circ } \right)\,$ A1 N1

[1 marks]

c.ii.

METHOD 1 ( $\frac{1}{2}$ × height × CD)

recognizing that OB is altitude of triangle with base CD (seen anywhere) M1

eg $\frac{1}{2} \times \left| {\mathop {{\text{OB}}}\limits^ \to } \right| \times \left| {\mathop {{\text{CD}}}\limits^ \to } \right|,\,\,{\text{OB}} \bot {\text{CD}},$ sketch showing right angle at B

$\mathop {{\text{CD}}}\limits^ \to = \left( \begin{gathered} - 6 \hfill \\ - 8 \hfill \\ \,5 \hfill \\ \end{gathered} \right)$ or $\mathop {{\text{DC}}}\limits^ \to = \left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right)$ (seen anywhere) (A1)

correct magnitudes (seen anywhere) (A1)(A1)

$\left| {\mathop {{\text{OB}}}\limits^ \to } \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 4} \right)}^2} + {{\left( { - 4} \right)}^2}} = \left( {\sqrt {36} } \right)$

$\left| {\mathop {{\text{CD}}}\limits^ \to } \right| = \sqrt {{{\left( { - 6} \right)}^2} + {{\left( { - 8} \right)}^2} + {{\left( 5 \right)}^2}} = \left( {\sqrt {125} } \right)$

correct substitution into $\frac{1}{2}bh$ A1

eg $\frac{1}{2} \times 6 \times \sqrt {125}$

area $= 3\sqrt {125} ,\,\,15\sqrt 5$ A1 N3

METHOD 2 (subtracting triangles)

recognizing that OB is altitude of either ΔOBD or ΔOBC(seen anywhere) M1

eg $\frac{1}{2} \times \left| {\mathop {{\text{OB}}}\limits^ \to } \right| \times \left| {\mathop {{\text{BD}}}\limits^ \to } \right|,\,\,{\text{OB}} \bot {\text{BC}},$ sketch of triangle showing right angle at B

one correct vector $\mathop {{\text{BD}}}\limits^ \to$ or $\mathop {{\text{DB}}}\limits^ \to$ or $\mathop {{\text{BC}}}\limits^ \to$ or $\mathop {{\text{CB}}}\limits^ \to$ (seen anywhere) (A1)

eg $\mathop {{\text{BD}}}\limits^ \to = \left( \begin{gathered} \,6 \hfill \\ \,8 \hfill \\ - 5 \hfill \\ \end{gathered} \right)$ , $\mathop {{\text{CB}}}\limits^ \to = \left( \begin{gathered} - 12 \hfill \\ - 16 \hfill \\ \,10 \hfill \\ \end{gathered} \right)$

$\left| {\mathop {{\text{OB}}}\limits^ \to } \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 4} \right)}^2} + {{\left( { - 4} \right)}^2}} = \left( {\sqrt {36} } \right)$ (seen anywhere) (A1)

one correct magnitude of a base (seen anywhere) (A1)

$\left| {\mathop {{\text{BD}}}\limits^ \to } \right| = \sqrt {{{\left( 6 \right)}^2} + {{\left( 8 \right)}^2} + {{\left( 5 \right)}^2}} = \left( {\sqrt {125} } \right),\,\,\left| {\mathop {{\text{BC}}}\limits^ \to } \right| = \sqrt {144 + 256 + 100} = \left( {\sqrt {500} } \right)$

correct working A1

eg $\frac{1}{2} \times 6 \times \sqrt {500} - \frac{1}{2} \times 6 \times 5\sqrt 5 ,\,\,\frac{1}{2} \times 6 \times \sqrt {500} \times {\text{sin}}90 - \frac{1}{2} \times 6 \times 5\sqrt 5 \times {\text{sin}}90$

area $= 3\sqrt {125} ,\,\,15\sqrt 5$ A1 N3

METHOD 3 (using $\frac{1}{2}$ ab sin C with ΔOCD)

two correct side lengths (seen anywhere) (A1)(A1)

$\left| {\mathop {{\text{OD}}}\limits^ \to } \right| = \sqrt {{{\left( 8 \right)}^2} + {{\left( 4 \right)}^2} + {{\left( { - 9} \right)}^2}} = \left( {\sqrt {161} } \right),\,\,\left| {\mathop {{\text{CD}}}\limits^ \to } \right| = \sqrt {{{\left( { - 6} \right)}^2} + {{\left( { - 8} \right)}^2} + {{\left( 5 \right)}^2}} = \left( {\sqrt {125} } \right),\,$ $\left| {\mathop {{\text{OC}}}\limits^ \to } \right| = \sqrt {{{\left( {14} \right)}^2} + {{\left( {12} \right)}^2} + {{\left( { - 14} \right)}^2}} = \left( {\sqrt {536} } \right)$

attempt to find cosine ratio (seen anywhere) M1
eg $\frac{{536 - 286}}{{ - 2\sqrt {161} \sqrt {125} }},\,\,\frac{{{\text{OD}} \bullet {\text{DC}}}}{{\left| {OD} \right|\left| {DC} \right|}}$

correct working for sine ratio A1

eg $\frac{{{{\left( {125} \right)}^2}}}{{161 \times 125}} + {\text{si}}{{\text{n}}^2}\,D = 1$

correct substitution into $\frac{1}{2}ab\,\,{\text{sin}}\,C$ A1

eg $0.5 \times \sqrt {161} \times \sqrt {125} \times \frac{6}{{\sqrt {161} }}$

area $= 3\sqrt {125} ,\,\,15\sqrt 5$ A1 N3

[6 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

Consider the function $f$ defined by $f (x) = 6 + 6 \cos x$ , for $0 \leq x \leq 4 π$ .

The following diagram shows the graph of $y = f (x)$ .

The graph of $f$ touches the $x$ -axis at points $A$ and $B$ , as shown. The shaded region is enclosed by the graph of $y = f (x)$ and the $x$ -axis, between the points $A$ and $B$ .

The right cone in the following diagram has a total surface area of $12 π$ , equal to the shaded area in the previous diagram.

The cone has a base radius of $2$ , height $h$ , and slant height $l$ .

Find the $x$ -coordinates of $A$ and $B$ .

[3]

Show that the area of the shaded region is $12 π$ .

[5]

Find the value of $l$ .

[3]

Hence, find the volume of the cone.

[4]

Markscheme

$6 + 6 \cos x = 0$ (or setting their $f' (x) = 0$ ) (M1)

$\cos x = - 1$ (or $\sin x = 0$ )

$x = π, x = 3 π$ A1A1

[3 marks]

attempt to integrate $\int_{π}^{3 π} (6 + 6 \cos x) d x$ (M1)

$= {[6 x + 6 \sin x]}_{π}^{3 π}$ A1A1

substitute their limits into their integrated expression and subtract (M1)

$= (18 π + 6 \sin 3 π) - (6 π + 6 \sin π)$

$= (6 (3 π) + 0) - (6 π + 0) (= 18 π - 6 π)$ A1

area $= 12 π$ AG

[5 marks]

attempt to substitute into formula for surface area (including base) (M1)

$π (2^{2}) + π (2) (l) = 12 π$ (A1)

$4 π + 2 π l = 12 π$

$2 π l = 8 π$

$l = 4$ A1

[3 marks]

valid attempt to find the height of the cone (M1)

e.g. $2^{2} + h^{2} = {(their l)}^{2}$

$h = \sqrt{12} (= 2 \sqrt{3})$ (A1)

attempt to use $V = \frac{1}{3} π r^{2} h$ with their values substituted M1

$(\frac{1}{3} π (2^{2}) (\sqrt{12}))$

$volume = \frac{4 π \sqrt{12}}{3} (= \frac{8 π \sqrt{3}}{3} = \frac{8 π}{\sqrt{3}})$ A1

[4 marks]

Examiners report

[N/A]

A calculator fits into a cuboid case with height 29 mm, width 98 mm and length 186 mm.

Find the volume, in cm³, of this calculator case.

Markscheme

evidence of 10 mm = 1 cm (A1)

Note: Award (A1) for dividing their volume from part (a) or part (b) by 1000.

529 (cm³) (528.612 (cm³)) (A1)(ft) (C2)

Note: Follow through from parts (a) or (b). Accept answers written in scientific notation.

[2 marks]

Examiners report

[N/A]

The following diagram shows a circle with centre $O$ and radius $r$ .

Points $A$ and $B$ lie on the circumference of the circle, and $A \hat{O} B = 1 radian$ .

The perimeter of the shaded region is $12$ .

Find the value of $r$ .

[3]

Hence, find the exact area of the non-shaded region.

[3]

Markscheme

minor arc $AB$ has length $r$ (A1)

recognition that perimeter of shaded sector is $3 r$ (A1)

$3 r = 12$

$r = 4$ A1

[3 marks]

EITHER
$θ = 2 π - A \hat{O} B (= 2 π - 1)$ (M1)

Area of non-shaded region $= \frac{1}{2} (2 π - 1) (4^{2})$ (A1)

area of circle $-$ area of shaded sector (M1)

$16 π - (\frac{1}{2} \times 1 \times 4^{2})$ (A1)

THEN

area $= 16 π - 8 (= 8 (2 π - 1))$ A1

[3 marks]

Examiners report

[N/A]

Show that ${\text{lo}}{{\text{g}}_9}\left( {{\text{cos}}\,2x + 2} \right) = {\text{lo}}{{\text{g}}_3}\sqrt {{\text{cos}}\,2x + 2}$ .

[3]

Hence or otherwise solve ${\text{lo}}{{\text{g}}_3}\left( {{\text{2}}\,{\text{sin}}\,x} \right) = {\text{lo}}{{\text{g}}_9}\left( {{\text{cos}}\,2x + 2} \right)$ for $0 < x < \frac{\pi }{2}$ .

[5]

Markscheme

attempting to use the change of base rule M1

${\text{lo}}{{\text{g}}_9}\left( {{\text{cos}}\,2x + 2} \right) = \frac{{{\text{lo}}{{\text{g}}_3}\left( {{\text{cos}}\,2x + 2} \right)}}{{{\text{lo}}{{\text{g}}_3}9}}$ A1

$= \frac{1}{2}{\text{lo}}{{\text{g}}_3}\left( {{\text{cos}}\,2x + 2} \right)$ A1

$= {\text{lo}}{{\text{g}}_3}\sqrt {{\text{cos}}\,2x + 2}$ AG

[3 marks]

${\text{lo}}{{\text{g}}_3}\left( {{\text{2}}\,{\text{sin}}\,x} \right) = {\text{lo}}{{\text{g}}_3}\sqrt {{\text{cos}}\,2x + 2}$

${\text{2}}\,{\text{sin}}\,x = \sqrt {{\text{cos}}\,2x + 2}$ M1

${\text{4}}\,{\text{si}}{{\text{n}}^2}\,x = {\text{cos}}\,2x + 2$ (or equivalent) A1

use of ${\text{cos}}\,2x = 1 - 2\,{\text{si}}{{\text{n}}^2}\,x$ (M1)

$6\,{\text{si}}{{\text{n}}^2}\,x = 3$

${\text{sin}}\,x = \left( \pm \right)\frac{1}{{\sqrt 2 }}$ A1

$x = \frac{\pi }{4}$ A1

Note: Award A0 if solutions other than $x = \frac{\pi }{4}$ are included.

[5 marks]

Examiners report

[N/A]

Given that ${\text{sin}}\,x = \frac{1}{3}$ , where $0 < x < \frac{\pi }{2}$ , find the value of ${\text{cos}}\,4x$ .

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

correct substitution into formula for ${\text{cos}}\,\left( {2x} \right)$ or ${\text{sin}}\,\left( {2x} \right)$ (A1)

eg $1 - 2{\left( {\frac{1}{3}} \right)^2}$ , $2{\left( {\frac{{\sqrt 8 }}{3}} \right)^2} - 1$ , $2\left( {\frac{1}{3}} \right)\left( {\frac{{\sqrt 8 }}{3}} \right)$ , ${\left( {\frac{{\sqrt 8 }}{3}} \right)^2} - {\left( {\frac{1}{3}} \right)^2}$

${\text{cos}}\,\left( {2x} \right) = \frac{7}{9}$ or ${\text{sin}}\,\left( {2x} \right) = \frac{{2\sqrt 8 }}{9}\,\,\,\,\left( { = \frac{{\sqrt {32} }}{9} = \frac{{4\sqrt 2 }}{9}} \right)$ (may be seen in substitution) A2

recognizing 4 $x$ is double angle of 2 $x$ (seen anywhere) (M1)

eg ${\text{cos}}\,\left( {2\left( {2x} \right)} \right)$ , $2\,{\text{co}}{{\text{s}}^2}\,\left( {2\theta } \right) - 1$ , $1 - 2\,{\text{si}}{{\text{n}}^2}\,\left( {2\theta } \right)$ , ${\text{co}}{{\text{s}}^2}\,\left( {2\theta } \right) - {\text{si}}{{\text{n}}^2}\,\left( {2\theta } \right)$

correct substitution of their value of ${\text{cos}}\,\left( {2x} \right)$ and/or ${\text{sin}}\,\left( {2x} \right)$ into formula for ${\text{cos}}\,\left( {4x} \right)$ (A1)

eg $2{\left( {\frac{7}{9}} \right)^2} - 1$ , $\frac{{98}}{{81}} - 1$ , $1 - 2{\left( {\frac{{2\sqrt 8 }}{9}} \right)^2}$ , $1 - \frac{{64}}{{81}}$ , ${\left( {\frac{7}{9}} \right)^2} - {\left( {\frac{{2\sqrt 8 }}{9}} \right)^2}$ , $\frac{{49}}{{81}} - \frac{{32}}{{81}}$

${\text{cos}}\,\left( {4x} \right) = \frac{{17}}{{81}}$ A1 N2

METHOD 2

recognizing 4 $x$ is double angle of 2 $x$ (seen anywhere) (M1)

eg ${\text{cos}}\,\left( {2\left( {2x} \right)} \right)$

double angle identity for 2 $x$ (M1)

eg $2\,{\text{co}}{{\text{s}}^2}\,\left( {2\theta } \right) - 1$ , $1 - 2\,{\text{si}}{{\text{n}}^2}\left( {2x} \right)$ , ${\text{co}}{{\text{s}}^2}\,\left( {2\theta } \right) - {\text{si}}{{\text{n}}^2}\,\left( {2\theta } \right)$

correct expression for ${\text{cos}}\,\left( {4x} \right)$ in terms of ${\text{sin}}\,x$ and/or ${\text{cos}}\,x$ (A1)

eg $2{\left( {1 - 2\,{\text{si}}{{\text{n}}^2}\,\theta } \right)^2} - 1$ , $1 - 2{\left( {2\,{\text{sin}}\,x\,{\text{cos}}\,x} \right)^2}$ , ${\left( {1 - 2\,{\text{si}}{{\text{n}}^2}\,\theta } \right)^2} - {\left( {2\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta } \right)^2}$

correct substitution for ${\text{sin}}\,x$ and/or ${\text{cos}}\,x$ A1

eg $2{\left( {1 - 2{{\left( {\frac{1}{3}} \right)}^2}} \right)^2} - 1$ , $2\left( {1 - 4{{\left( {\frac{1}{3}} \right)}^2} + 4{{\left( {\frac{1}{3}} \right)}^4}} \right) - 1$ , $1 - 2{\left( {2 \times \frac{1}{3} \times \frac{{\sqrt 8 }}{3}} \right)^2}$

correct working (A1)

eg $2\left( {\frac{{49}}{{81}}} \right) - 1$ , $1 - 2\left( {\frac{{32}}{{81}}} \right)$ , $\frac{{49}}{{81}} - \frac{{32}}{{81}}$

${\text{cos}}\,\left( {4x} \right) = \frac{{17}}{{81}}$ A1 N2

[6 marks]

Examiners report

[N/A]

Note: In this question, distance is in metres and time is in seconds.

Two particles ${P_1}$ and ${P_2}$ start moving from a point A at the same time, along different straight lines.

After $t$ seconds, the position of ${P_1}$ is given by r = $\left( {\begin{array}{*{20}{c}} 4 \\ { - 1} \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { - 1} \end{array}} \right)$ .

Two seconds after leaving A, ${P_1}$ is at point B.

Two seconds after leaving A, ${P_2}$ is at point C, where $\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 0 \\ 4 \end{array}} \right)$ .

Find the coordinates of A.

[2]

Find $\overrightarrow {{\text{AB}}}$ ;

[3]

b.i.

Find $\left| {\overrightarrow {{\text{AB}}} } \right|$ .

[2]

b.ii.

Find $\cos {\rm{B\hat AC}}$ .

[5]

Hence or otherwise, find the distance between ${P_1}$ and ${P_2}$ two seconds after they leave A.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

recognizing $t = 0$ at A (M1)

A is $(4,{\text{ }} - 1,{\text{ }}3)$ A1 N2

[2 marks]

METHOD 1

valid approach (M1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} 4 \\ { - 1} \\ 3 \end{array}} \right) + 2\left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { - 2} \end{array}} \right),{\text{ }}(6,{\text{ }}3,{\text{ }} - 1)$

correct approach to find $\overrightarrow {{\text{AB}}}$ (A1)

eg $\,\,\,\,\,$ ${\text{AO}} + {\text{OB}},{\text{ B}} - {\text{A, }}\left( {\begin{array}{*{20}{c}} 6 \\ 3 \\ { - 1} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 4 \\ { - 1} \\ 3 \end{array}} \right)$

$\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { - 4} \end{array}} \right)$ A1 N2

METHOD 2

recognizing $\overrightarrow {{\text{AB}}}$ is two times the direction vector (M1)

correct working (A1)

eg $\,\,\,\,\,$ $\overrightarrow {{\text{AB}}} = 2\left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { - 2} \end{array}} \right)$

$\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { - 4} \end{array}} \right)$ A1 N2

[3 marks]

b.i.

correct substitution (A1)

eg $\,\,\,\,\,$ $\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt {{2^2} + {4^2} + {4^2}} ,{\text{ }}\sqrt {4 + 16 + 16} ,{\text{ }}\sqrt {36}$

$\left| {\overrightarrow {{\text{AB}}} } \right| = 6$ A1 N2

[2 marks]

b.ii.

METHOD 1 (vector approach)

valid approach involving $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{AC}}}$ (M1)

eg $\,\,\,\,\,$ $\overrightarrow {{\text{AB}}} \bullet \overrightarrow {{\text{AC}}} ,{\text{ }}\frac{{\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{AC}}} }}{{{\text{AB}} \times {\text{AC}}}}$

finding scalar product and $\left| {\overrightarrow {{\text{AC}}} } \right|$ (A1)(A1)

scalar product $2(3) + 4(0) - 4(4){\text{ }}( = - 10)$

$\left| {\overrightarrow {{\text{AC}}} } \right| = \sqrt {{3^2} + {0^2} + {4^2}} {\text{ }}( = 5)$

substitution of their scalar product and magnitudes into cosine formula (M1)

eg $\,\,\,\,\,$ $\cos {\rm{B\hat AC = }}\frac{{6 + 0 - 16}}{{6\sqrt {{3^2} + {4^2}} }}$

${\text{cos}}\,B\hat AC = - \frac{{10}}{{30}}\left( { = - \frac{1}{3}} \right)$ A1 N2

METHOD 2 (triangle approach)

valid approach involving cosine rule (M1)

eg $\,\,\,\,\,$ $\cos {\rm{B\hat AC = }}\frac{{{\text{A}}{{\text{B}}^2} + {\text{A}}{{\text{C}}^2} - {\text{B}}{{\text{C}}^2}}}{{2 \times {\text{AB}} \times {\text{AC}}}}$

finding lengths AC and BC (A1)(A1)

${\text{AC}} = 5,{\text{ BC}} = 9$

substitution of their lengths into cosine formula (M1)

eg $\,\,\,\,\,$ $\cos {\rm{B\hat AC}} = \frac{{{5^2} + {6^2} - {9^2}}}{{2 \times 5 \times 6}}$

$\cos {\rm{B\hat AC}} = - \frac{{20}}{{60}}{\text{ }}\left( { = - \frac{1}{3}} \right)$ A1 N2

[5 marks]

Note: Award relevant marks for working seen to find BC in part (c) (if cosine rule used in part (c)).

METHOD 1 (using cosine rule)

recognizing need to find BC (M1)

choosing cosine rule (M1)

eg $\,\,\,\,\,$ ${c^2} = {a^2} + {b^2} - 2ab\cos {\text{C}}$

correct substitution into RHS A1

eg $\,\,\,\,\,$ ${\text{B}}{{\text{C}}^2} = {(6)^2} + {(5)^2} - 2(6)(5)\left( { - \frac{1}{3}} \right),{\text{ }}36 + 25 + 20$

distance is 9 A1 N2

METHOD 2 (finding magnitude of $\overrightarrow {BC}$ )

recognizing need to find BC (M1)

valid approach (M1)

eg $\,\,\,\,\,$ attempt to find $\overrightarrow {{\rm{OB}}}$ or $\overrightarrow {{\rm{OC}}}$ , $\overrightarrow {{\rm{OB}}} = \left( {\begin{array}{*{20}{c}} 6 \\ 3 \\ { - 1} \end{array}} \right)$ or $\overrightarrow {{\rm{OC}}} = \left( {\begin{array}{*{20}{c}} 7 \\ { - 1} \\ 7 \end{array}} \right),{\text{ }}\overrightarrow {{\rm{BA}}} + \overrightarrow {{\rm{AC}}}$

correct working A1

eg $\,\,\,\,\,$ $\overrightarrow {{\rm{BC}}} = \left( {\begin{array}{*{20}{c}} 1 \\ { - 4} \\ 8 \end{array}} \right),{\text{ }}\overrightarrow {{\rm{CB}}} = \left( {\begin{array}{*{20}{c}} { - 1} \\ 4 \\ { - 8} \end{array}} \right),{\text{ }}\sqrt {{1^2} + {4^2} + {8^2}} = \sqrt {81}$

distance is 9 A1 N2

METHOD 3 (finding coordinates and using distance formula)

recognizing need to find BC (M1)

valid approach (M1)

eg $\,\,\,\,\,$ attempt to find coordinates of B or C, ${\text{B}}(6,{\text{ }}3,{\text{ }} - 1)$ or ${\text{C}}(7,{\text{ }} - 1,{\text{ }}7)$

correct substitution into distance formula A1

eg $\,\,\,\,\,$ ${\text{BC}} = \sqrt {{{(6 - 7)}^2} + {{\left( {3 - ( - 1)} \right)}^2} + {{( - 1 - 7)}^2}} ,{\text{ }}\sqrt {{1^2} + {4^2} + {8^2}} = \sqrt {81}$

distance is 9 A1 N2

[4 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

A ladder on a fire truck has its base at point B which is 4 metres above the ground. The ladder is extended and its other end rests on a vertical wall at point C, 16 metres above the ground. The horizontal distance between B and C is 9 metres.

Find the angle of elevation from B to C.

[3]

A second truck arrives whose ladder, when fully extended, is 30 metres long. The base of this ladder is also 4 metres above the ground. For safety reasons, the maximum angle of elevation that the ladder can make is 70º.

Find the maximum height on the wall that can be reached by the ladder on the second truck.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${\text{tan}}\,B = \frac{{12}}{9}$ (A1)(M1)

Note: Award (A1) for 12 seen, (M1) for correct substitution into tan (or equivalent). Accept equivalent methods, such as Pythagoras, to find BC and correct substitution into other trig ratios. If ${\text{ta}}{{\text{n}}^{ - 1}}\left( {\frac{{16}}{9}} \right)$ seen award (A0)(M1)(A0).

53.1° (53.1301…°) (A1) (C3)

Note: If radians are used the answer is 0.927295…; award at most (A1)(M1)(A0).

[3 marks]

$30\,{\text{sin}}\,70^\circ + 4$ (M1)(M1)

Note: Award (M1) for ${\text{sin}}\,70^\circ = \frac{x}{{30}}$ (or equivalent) and (M1) for adding 4.

32.2 (32.1907…) (m) (A1) (C3)

Note: If radians are used the answer is 27.2167…; award at most (M1)(M1)(A0).

[3 marks]

Examiners report

[N/A]

Let $\mathop {{\text{OA}}}\limits^ \to = \left( \begin{gathered} 2 \hfill \\ 1 \hfill \\ 3 \hfill \\ \end{gathered} \right)$ and $\mathop {{\text{AB}}}\limits^ \to = \left( \begin{gathered} 1 \hfill \\ 3 \hfill \\ 1 \hfill \\ \end{gathered} \right)$ , where O is the origin. L₁ is the line that passes through A and B.

Find a vector equation for L₁.

[2]

The vector $\left( \begin{gathered} 2 \hfill \\ p \hfill \\ 0 \hfill \\ \end{gathered} \right)$ is perpendicular to $\mathop {{\text{AB}}}\limits^ \to$ . Find the value of p.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

any correct equation in the form r = a + tb (accept any parameter for t)

where a is $\left( \begin{gathered} 2 \hfill \\ 1 \hfill \\ 3 \hfill \\ \end{gathered} \right)$ , and b is a scalar multiple of $\left( \begin{gathered} 1 \hfill \\ 3 \hfill \\ 1 \hfill \\ \end{gathered} \right)$ A2 N2

eg r = $\left( \begin{gathered} 2 \hfill \\ 1 \hfill \\ 3 \hfill \\ \end{gathered} \right) = t\left( \begin{gathered} 1 \hfill \\ 3 \hfill \\ 1 \hfill \\ \end{gathered} \right)$ , r = 2i + j + 3k + s(i + 3j + k)

Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.

[2 marks]

METHOD 1

correct scalar product (A1)

eg (1 × 2) + (3 × p) + (1 × 0), 2 + 3p

evidence of equating their scalar product to zero (M1)

eg a•b = 0, 2 + 3p = 0, 3p = −2

$p = - \frac{2}{3}$ A1 N3

METHOD 2

valid attempt to find angle between vectors (M1)

correct substitution into numerator and/or angle (A1)

eg ${\text{cos}}\,\theta = \frac{{\left( {1 \times 2} \right) + \left( {3 \times p} \right) + \left( {1 \times 0} \right)}}{{\left| a \right|\left| b \right|}},\,\,{\text{cos}}\,\theta = 0$

$p = - \frac{2}{3}$ A1 N3

[3 marks]

Examiners report

[N/A]

A park in the form of a triangle, ABC, is shown in the following diagram. AB is 79 km and BC is 62 km. Angle A $\mathop {\text{B}}\limits^ \wedge$ C is 52°.

Calculate the length of side AC in km.

[3]

Calculate the area of the park.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(AC² =) 62² + 79² − 2 × 62 × 79 × cos(52°) (M1)(A1)

Note: Award (M1) for substituting in the cosine rule formula, (A1) for correct substitution.

63.7 (63.6708…) (km) (A1) (C3)

[3 marks]

$\frac{1}{2}$ × 62 × 79 × sin(52°) (M1)(A1)

Note: Award (M1) for substituting in the area of triangle formula, (A1) for correct substitution.

1930 km² (1929.83…km²) (A1) (C3)

[3 marks]

Examiners report

[N/A]

The vectors a = $\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right)$ and b = $\left( {\begin{array}{*{20}{c}} {k + 3} \\ k \end{array}} \right)$ are perpendicular to each other.

Find the value of $k$ .

[4]

Given that c = a + 2b, find c.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of scalar product M1

eg $\,\,\,\,\,$ a $\bullet$ b, $4(k + 3) + 2k$

recognizing scalar product must be zero (M1)

eg $\,\,\,\,\,$ a $\bullet$ b $= 0,{\text{ }}4k + 12 + 2k = 0$

correct working (must involve combining terms) (A1)

eg $6k + 12,\,\,\,6k = - 12$

$\,\,\,\,\,$ $k = - 2$ A1 N2

[4 marks]

attempt to substitute their value of $k$ (seen anywhere) (M1)

eg $\,\,\,\,\,$ b = $\left( {\begin{array}{*{20}{c}} { - 2 + 3} \\ { - 2} \end{array}} \right)$ , 2b = $\left( {\begin{array}{*{20}{c}} 2 \\ { - 4} \end{array}} \right)$

correct working (A1)

eg $\,\,\,\,\,$ $\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2 \\ { - 4} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} {4 + 2k + 6} \\ {2 + 2k} \end{array}} \right)$

c = $\left( {\begin{array}{*{20}{c}} 6 \\ { - 2} \end{array}} \right)$ A1 N2

[3 marks]

Examiners report

[N/A]

Two fixed points, A and B, are 40 m apart on horizontal ground. Two straight ropes, AP and BP, are attached to the same point, P, on the base of a hot air balloon which is vertically above the line AB. The length of BP is 30 m and angle BAP is 48°.

Angle APB is acute.

On the diagram, draw and label with an x the angle of depression of B from P.

[1]

Find the size of angle APB.

[3]

Find the size of the angle of depression of B from P.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(A1) (C1)

[1 mark]

$\frac{{40}}{{{\text{sin APB}}}} = \frac{{30}}{{{\text{sin 48}}^\circ }}$ (M1)(A1)

Note: Award (M1) for substitution into sine rule, (A1) for correct substitution.

(angle APB =) 82.2° (82.2473…°) (A1) (C3)

[3 marks]

180 − 48 − 82.2473… (M1)

49.8° (49.7526…°) (A1)(ft) (C2)

Note: Follow through from parts (a) and (b).

[2 marks]

Examiners report

[N/A]

A line, ${L_1}$ , has equation $r = \left( {\begin{array}{*{20}{c}} { - 3} \\ 9 \\ {10} \end{array}} \right) + s\left( {\begin{array}{*{20}{c}} 6 \\ 0 \\ 2 \end{array}} \right)$ . Point ${\text{P}}\left( {15{\text{,}}\,\,9{\text{,}}\,\,c} \right)$ lies on ${L_1}$ .

Find $c$ .

[4]

A second line, ${L_2}$ , is parallel to ${L_1}$ and passes through (1, 2, 3).

Write down a vector equation for ${L_2}$ .

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct equation (A1)

eg $- 3 + 6s = 15$ , $6s = 18$

$s = 3$ (A1)

substitute their $s$ value into $z$ component (M1)

eg $10 + 3\left( 2 \right)$ , $10 + 6$

$c = 16$ A1 N3

[4 marks]

$r = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 6 \\ 0 \\ 2 \end{array}} \right)$ (=(i + 2j + 3k) + $t$ (6i + 2k)) A2 N2

Note: Accept any scalar multiple of $\left( {\begin{array}{*{20}{c}} 6 \\ 0 \\ 2 \end{array}} \right)$ for the direction vector.

Award A1 for $\left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 6 \\ 0 \\ 2 \end{array}} \right)$ , A1 for ${L_2} = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 6 \\ 0 \\ 2 \end{array}} \right)$ , A0 for $r = \left( {\begin{array}{*{20}{c}} 6 \\ 0 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \end{array}} \right)$ .

[2 marks]

Examiners report

[N/A]

Consider the functions $f (x) = \sqrt{3} \sin x + \cos x$ where $0 \leq x \leq π$ and $g (x) = 2 x$ where $x \in ℝ$ .

Find $(f \circ g) (x)$ .

[2]

Solve the equation $(f \circ g) (x) = 2 \cos 2 x$ where $0 \leq x \leq π$ .

[5]

Markscheme

$(f \circ g) (x) = f (2 x)$ (A1)

$f (2 x) = \sqrt{3} \sin 2 x + \cos 2 x$ A1

[2 marks]

$\sqrt{3} \sin 2 x + \cos 2 x = 2 \cos 2 x$

$\sqrt{3} \sin 2 x = \cos 2 x$

recognising to use $\tan$ or $cot$ M1

$\tan 2 x = \frac{1}{\sqrt{3}}$ OR $cot 2 x = \sqrt{3}$ (values may be seen in right triangle) (A1)

$(arctan (\frac{1}{\sqrt{3}}) =) \frac{π}{6}$ (seen anywhere) (accept degrees) (A1)

$2 x = \frac{π}{6}, \frac{7 π}{6}$

$x = \frac{π}{12}, \frac{7 π}{12}$ A1A1

Note: Do not award the final A1 if any additional solutions are seen.
Award A1A0 for correct answers in degrees.
Award A0A0 for correct answers in degrees with additional values.

[5 marks]

Examiners report

Determining the composite function was very well done. In part (b) very few candidates showed any recognition that tan (or cot) were required to solve this trigonometric equation. Many saw the 2x and simply employed one of the double angle rules but could not then progress to an answer.

[N/A]

Consider the vectors a = $\left( {\begin{array}{*{20}{c}} 3 \\ {2p} \end{array}} \right)$ and b = $\left( {\begin{array}{*{20}{c}} {p + 1} \\ 8 \end{array}} \right)$ .

Find the possible values of p for which a and b are parallel.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1 (eliminating k)

recognizing parallel vectors are multiples of each other (M1)

eg a = kb, $\left( {\begin{array}{*{20}{c}} 3 \\ {2p} \end{array}} \right)$ = k $\left( {\begin{array}{*{20}{c}} {p + 1} \\ 8 \end{array}} \right)$ , $\frac{{p + 1}}{3} = \frac{8}{{2p}}$ , 3k = p + 1 and 2kp = 8

correct working (must be quadratic) (A1)

eg 2p² + 2p = 24, p² + p – 12, $3 = \frac{{{p^2} + p}}{4}$

valid attempt to solve their quadratic equation (M1)

eg factorizing, formula, completing the square

evidence of correct working (A1)

eg (p + 4)(p – 3), $x = \frac{{ - 2 \pm \sqrt {4 - 4\left( 2 \right)\left( { - 24} \right)} }}{4}$

p = –4, p = 3 A1A1 N4

METHOD 2 (solving for k)

recognizing parallel vectors are multiples of each other (M1)

eg a = kb, $\left( {\begin{array}{*{20}{c}} 3 \\ {2p} \end{array}} \right)$ = k $\left( {\begin{array}{*{20}{c}} {p + 1} \\ 8 \end{array}} \right)$ , 3k = p + 1 and 2kp = 8

correct working (must be quadratic) (A1)

eg 3k² – k = 4, 3k² – k – 4, 4k² = 3 – k

one correct value for k (A1)

eg k = –1, k = $\frac{4}{3}$ , k = $\frac{3}{4}$

substituting their value(s) of k (M1)

eg $\left( {\begin{array}{*{20}{c}} 3 \\ {2p} \end{array}} \right) = \frac{3}{4}\left( {\begin{array}{*{20}{c}} {p + 1} \\ 8 \end{array}} \right)$ , $3\left( {\frac{4}{3}} \right) = p + 1$ and $2\left( {\frac{4}{3}} \right)p = 8$ , $\left( { - 1} \right)\left( {\begin{array}{*{20}{c}} 3 \\ {2p} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {p + 1} \\ 8 \end{array}} \right)$

p = –4, p = 3 A1A1 N4

METHOD 3 (working with angles and cosine formula)

recognizing angle between parallel vectors is 0 and/or 180° M1

eg cos θ = ±1, $a \bullet b = \left| a \right|\left| b \right|$

correct substitution of scalar product and magnitudes into equation (A1)

eg $\frac{{3\left( {p + 1} \right) + 2p\left( 8 \right)}}{{\sqrt {{3^2} + {{\left( {2p} \right)}^2}} \sqrt {{{\left( {p + 1} \right)}^2} + {8^2}} }} = \pm 1$ , $19p + 3 = \sqrt {4{p^2} + 9} \sqrt {{p^2} + 2p + 65}$

correct working (must include both ± ) (A1)

eg $3\left( {p + 1} \right) + 2p\left( 8 \right) = \pm \sqrt {{3^2} + {{\left( {2p} \right)}^2}} \sqrt {{{\left( {p + 1} \right)}^2} + {8^2}}$ , $19p + 3 = \pm \sqrt {4{p^2} + 9} \sqrt {{p^2} + 2p + 65}$

correct quartic equation (A1)

eg $361\,{p^2} + 114p + 9 = 4{p^4} + 8{p^3} + 269{p^2} + 18p + 585$ , $4{p^4} + 8{p^3} - 92{p^2} - 96p + 576 = 0$ , ${p^4} + 2{p^3} - 23{p^2} - 24p + 144 = 0$ , ${\left( {p + 4} \right)^2}{\left( {p - 3} \right)^2} = 0$

p = –4, p = 3 A2 N4

[6 marks]

Examiners report

[N/A]

Consider the graph of the function $f\left( x \right) = 2\,{\text{sin}}\,x$ , 0 ≤ $x$ < $2\pi$ . The graph of $f$ intersects the line $y = - 1$ exactly twice, at point A and point B. This is shown in the following diagram.

Consider the graph of $g\left( x \right) = 2\,{\text{sin}}\,px$ , 0 ≤ $x$ < $2\pi$ , where $p$ > 0.

Find the greatest value of $p$ such that the graph of $g$ does not intersect the line $y = - 1$ .

Markscheme

recognizing period of $g$ is larger than the period of $f$ (M1)

eg sketch of $g$ with larger period (may be seen on diagram), A at $x = 2\pi$ ,

image of A when $x > 2\pi$ , $\frac{{7\pi }}{6} \to 2\pi$ , $2\,{\text{sin}}\,\left( {2\pi p} \right) = - 1$ , $\frac{{7\pi }}{6} \times k = 2\pi$

correct working (A1)

eg $\frac{{7\pi }}{6} \cdot \frac{1}{p} = 2\pi$ , $2\pi p = \frac{{7\pi }}{6}$ , $\frac{{12}}{7}$

$p = \frac{7}{12}$ $\left( {{\text{accept}}\,\,p < \frac{7}{12}\,\,{\text{or}}\,\,p \leqslant \frac{7}{12}} \right)$ A1 N2

[3 marks]

Examiners report

[N/A]

A buoy is floating in the sea and can be seen from the top of a vertical cliff. A boat is travelling from the base of the cliff directly towards the buoy.

The top of the cliff is 142 m above sea level. Currently the boat is 100 metres from the buoy and the angle of depression from the top of the cliff to the boat is 64°.

Draw and label the angle of depression on the diagram.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(A1) (C1)

Note: The horizontal line must be shown and the angle of depression must be labelled. Accept a numerical or descriptive label.

[1 mark]

Examiners report

[N/A]

The following diagram shows a triangle $ABC$ .

$AC = 15 cm, BC = 10 cm$ , and $A \hat{B} C = θ$ .

Let $\sin C \hat{A} B = \frac{\sqrt{3}}{3}$ .

Given that $A \hat{B} C$ is acute, find $\sin θ$ .

[3]

Find $\cos (2 \times C \hat{A} B)$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1 – (sine rule)

evidence of choosing sine rule (M1)

eg $\frac{\sin \hat{A}}{a} = \frac{\sin \hat{B}}{b}$

correct substitution (A1)

eg $\frac{\frac{\sqrt{3}}{3}}{10} = \frac{\sin θ}{15}, \frac{\sqrt{3}}{30} = \frac{\sin θ}{15}, \frac{\sqrt{3}}{30} = \frac{\sin B}{15}$

$\sin θ = \frac{\sqrt{3}}{2}$ A1 N2

METHOD 2 – (perpendicular from vertex $C$ )

valid approach to find perpendicular length (may be seen on diagram) (M1)

eg , $\frac{h}{15} = \frac{\sqrt{3}}{3}$

correct perpendicular length (A1)

eg $\frac{15 \sqrt{3}}{3}, 5 \sqrt{3}$

$\sin θ = \frac{\sqrt{3}}{2}$ A1 N2

Note: Do not award the final A mark if candidate goes on to state $\sin θ = \frac{π}{3}$ , as this demonstrates a lack of understanding.

[3 marks]

attempt to substitute into double-angle formula for cosine (M1)

$1 - 2 {(\frac{\sqrt{3}}{3})}^{2}, 2 {(\frac{\sqrt{6}}{3})}^{2} - 1, {(\frac{\sqrt{6}}{3})}^{2} - {(\frac{\sqrt{3}}{3})}^{2}, \cos (2 θ) = 1 - 2 {(\frac{\sqrt{3}}{2})}^{2}, 1 - 2 \sin^{2} (\frac{\sqrt{3}}{3})$

correct working (A1)

eg $1 - 2 \times \frac{3}{9}, 2 \times \frac{6}{9} - 1, \frac{6}{9} - \frac{3}{9}$

$\cos (2 \times C \hat{A} B) = \frac{3}{9} (= \frac{1}{3})$ A1 N2

[3 marks]

Examiners report

[N/A]

The magnitudes of two vectors, u and v, are 4 and $\sqrt 3$ respectively. The angle between u and v is $\frac{\pi }{6}$ .

Let w = u − v. Find the magnitude of w.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1 (cosine rule)

diagram including u, v and included angle of $\frac{\pi }{6}$ (M1)

sketch of triangle with w (does not need to be to scale) (A1)

choosing cosine rule (M1)

eg ${a^2} + {b^2} - 2ab\,{\text{cos}}\,C$

correct substitution A1

eg ${4^2} + {\left( {\sqrt 3 } \right)^2} - 2\left( 4 \right)\left( {\sqrt 3 } \right){\text{cos}}\frac{\pi }{6}$

${\text{cos}}\frac{\pi }{6} = \frac{{\sqrt 3 }}{2}$ (seen anywhere) (A1)

correct working (A1)

eg 16 + 3 − 12

| w | = $\sqrt 7$ A1 N2

METHOD 2 (scalar product)

valid approach, in terms of u and v (seen anywhere) (M1)

eg | w |² = (u − v)•(u − v), | w |² = u•u − 2u•v + v•v, | w |²= ${\left( {{u_1} - {v_1}} \right)^2} + {\left( {{u_2}\; - \;{v_2}} \right)^2}$ ,

| w | = $\sqrt {{{\left( {{u_1} - {v_1}} \right)}^2} + {{\left( {{u_2}\; - \;{v_2}} \right)}^2} + {{\left( {{u_3}\; - \;{v_3}} \right)}^2}}$

correct value for u•u (seen anywhere) (A1)

eg | u |² = 16, u•u = 16, ${u_1}^2 + {u_2}^2 = 16$

correct value for v•v (seen anywhere) (A1)

eg | v |² = 16, v•v = 3, ${v_1}^2 + {v_2}^2 + {v_3}^2 = 3$

${\text{cos}}\left( {\frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{2}$ (seen anywhere) (A1)

u•v $= 4 \times \sqrt 3 \times \frac{{\sqrt 3 }}{2}$ (= 6) (seen anywhere) A1

correct substitution into u•u − 2u•v + v•v or ${u_1}^2 + {u_2}^2 + {v_1}^2 + {v_2}^2 - 2\left( {{u_1}{v_1} + {u_2}{v_2}} \right)$ (2 or 3 dimensions) (A1)

eg 16 − 2(6) + 3 (= 7)

| w | = $\sqrt 7$ A1 N2

Examiners report

[N/A]

Julio is making a wooden pencil case in the shape of a large pencil. The pencil case consists of a cylinder attached to a cone, as shown.

The cylinder has a radius of r cm and a height of 12 cm.

The cone has a base radius of r cm and a height of 10 cm.

Find an expression for the slant height of the cone in terms of r.

[2]

The total external surface area of the pencil case rounded to 3 significant figures is 570 cm².

Using your graphic display calculator, calculate the value of r.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(slant height² =) 10² + r ² (M1)

Note: For correct substitution of 10 and r into Pythagoras’ Theorem.

$\sqrt {{{10}^2} + {r^2}}$ (A1) (C2)

[2 marks]

$\pi {r^2} + 2\pi r \times 12 + \pi r\sqrt {100 + {r^2}} = 570$ (M1)(M1)(M1)

Note: Award (M1) for correct substitution in curved surface area of cylinder and area of the base, (M1) for their correct substitution in curved surface area of cone, (M1) for adding their 3 surface areas and equating to 570. Follow through their part (a).

= 4.58 (4.58358...) (A1)(ft) (C4)

Note: Last line must be seen to award final (A1). Follow through from part (a).

[4 marks]

Examiners report

[N/A]

Let $f\left( x \right) = 4\,{\text{cos}}\left( {\frac{x}{2}} \right) + 1$ , for $0 \leqslant x \leqslant 6\pi$ . Find the values of $x$ for which $f\left( x \right) > 2\sqrt 2 + 1$ .

Markscheme

METHOD 1 – FINDING INTERVALS FOR x

$4\,{\text{cos}}\left( {\frac{x}{2}} \right) + 1 > 2\sqrt 2 + 1$

correct working (A1)

eg $4\,{\text{cos}}\left( {\frac{x}{2}} \right) = 2\sqrt 2$ , ${\text{cos}}\left( {\frac{x}{2}} \right) > \frac{{\sqrt 2 }}{2}$

recognizing ${\text{co}}{{\text{s}}^{ - 1}}\frac{{\sqrt 2 }}{2} = \frac{\pi }{4}$ (A1)

one additional correct value for $\frac{x}{2}$ (ignoring domain and equation/inequalities) (A1)

eg $- \frac{\pi }{4}{\text{, }}\frac{{7\pi }}{4}{\text{, }}315^\circ {\text{, }}\frac{{9\pi }}{4}{\text{, }} - 45^\circ {\text{, }}\frac{{15\pi }}{4}$

three correct values for $x$ A1A1

eg $\frac{\pi }{2}{\text{, }}\frac{{7\pi }}{2}{\text{, }}\frac{{9\pi }}{2}$

valid approach to find intervals (M1)

correct intervals (must be in radians) A1A1 N2

$0 \leqslant x < \frac{\pi }{2}$ , $\frac{{7\pi }}{2} < x < \frac{{9\pi }}{2}$

Note: If working shown, award A1A0 if inclusion/exclusion of endpoints is incorrect. If no working shown award N1.
If working shown, award A1A0 if both correct intervals are given, and additional intervals are given. If no working shown award N1.
Award A0A0 if inclusion/exclusion of endpoints are incorrect and additional intervals are given.

METHOD 2 – FINDING INTERVALS FOR $\frac{x}{2}$

$4\,{\text{cos}}\left( {\frac{x}{2}} \right) + 1 > 2\sqrt 2 + 1$

correct working (A1)

eg $4\,{\text{cos}}\left( {\frac{x}{2}} \right) = 2\sqrt 2$ , ${\text{cos}}\left( {\frac{x}{2}} \right) > \frac{{\sqrt 2 }}{2}$

recognizing ${\text{co}}{{\text{s}}^{ - 1}}\frac{{\sqrt 2 }}{2} = \frac{\pi }{4}$ (A1)

one additional correct value for $\frac{x}{2}$ (ignoring domain and equation/inequalities) (A1)

eg $- \frac{\pi }{4}{\text{, }}\frac{{7\pi }}{4}{\text{, }}315^\circ {\text{, }}\frac{{9\pi }}{4}{\text{, }} - 45^\circ {\text{, }}\frac{{15\pi }}{4}$

three correct values for $\frac{x}{2}$ A1

eg $\frac{\pi }{4}{\text{, }}\frac{{7\pi }}{4}{\text{, }}\frac{{9\pi }}{4}$

valid approach to find intervals (M1)

one correct interval for $\frac{x}{2}$ A1

eg $0 \leqslant \frac{x}{2} < \frac{\pi }{4}{\text{, }}\frac{{7\pi }}{4} < \frac{x}{2} < \frac{{9\pi }}{4}$

correct intervals (must be in radians) A1A1 N2

$0 \leqslant x < \frac{\pi }{2}$ , $\frac{{7\pi }}{2} < x < \frac{{9\pi }}{2}$

[8 marks]

Examiners report

[N/A]

The following diagram shows triangle PQR.

M17/5/MATME/SP1/ENG/TZ1/03

Find PR.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

evidence of choosing the sine rule (M1)

eg $\,\,\,\,\,$ $\frac{a}{{\sin A}} = \frac{b}{{\sin B}}$

correct substitution A1

eg $\,\,\,\,\,$ $\frac{x}{{\sin 30}} = \frac{{13}}{{\sin 45}},{\text{ }}\frac{{13\sin 30}}{{\sin 45}}$

$\sin 30 = \frac{1}{2},{\text{ }}\sin 45 = \frac{1}{{\sqrt 2 }}$ (A1)(A1)

correct working A1

eg $\,\,\,\,\,$ $\frac{1}{2} \times \frac{{13}}{{\frac{1}{{\sqrt 2 }}}},{\text{ }}\frac{1}{2} \times 13 \times \frac{2}{{\sqrt 2 }},{\text{ }}13 \times \frac{1}{2} \times \sqrt 2$

correct answer A1 N3

eg $\,\,\,\,\,$ ${\text{PR}} = \frac{{13\sqrt 2 }}{2},{\text{ }}\frac{{13}}{{\sqrt 2 }}{\text{ (cm)}}$

METHOD 2 (using height of ΔPQR)

valid approach to find height of ΔPQR (M1)

eg $\,\,\,\,\,$ $\sin 30 = \frac{x}{{13}},{\text{ }}\cos 60 = \frac{x}{{13}}$

$\sin 30 = \frac{1}{2}{\text{ or }}\cos 60 = \frac{1}{2}$ (A1)

${\text{height}} = 6.5$ A1

correct working A1

eg $\,\,\,\,\,$ $\sin 45 = \frac{{6.5}}{{{\text{PR}}}},{\text{ }}\sqrt {{{6.5}^2} + {{6.5}^2}}$

correct working (A1)

eg $\,\,\,\,\,$ $\sin 45 = \frac{1}{{\sqrt 2 }},{\text{ }}\cos 45 = \frac{1}{{\sqrt 2 }},{\text{ }}\sqrt {\frac{{169 \times 2}}{4}}$

correct answer A1 N3

eg $\,\,\,\,\,$ ${\text{PR}} = \frac{{13\sqrt 2 }}{2},{\text{ }}\frac{{13}}{{\sqrt 2 }}{\text{ (cm)}}$

[6 marks]

Examiners report

[N/A]